domingo, 7 de noviembre de 2010

Fundamento

http://videos-de-dibujo-tecnico-y-geometria.blogspot.com.es/

El sistema diédrico es un método de representación de proyecciones múltiples, en el que los elementos quedan definidos por sus proyecciones ortogonales sobre al menos dos planos de proyección.
Los planos de proyección de los que nos valemos generalmente son 3: planta, alzado y perfil. Una vez que se han proyectado sobre cada unos de ellos las vistas ortogonales del objeto, se giran hasta hacerlos coincidir los tres en un mismo plano.

En la figura un cilindro se proyecta punto por punto sobre el plano horizontal PH y el vertical PV. Como se hace mediante perpendiculares, la circunferencia de la base se transforma en el alzado en una línea recta, por ser el plano que la contiene perpendicular al plano vertical.
Por ser paralela a la planta, la cara superior del cilindro se transforma sobre este plano en un círculo igual.
La recta de intersección del plano vertical y horizontal se llama línea de tierra.













A continuación se gira el plano vertical 90º hasta hacerlo coincidir con el horizontal tomando como eje de giro la línea de tierra. El giro provoca que las dos vistas queden perfectamente alineadas en líneas ortogonales a la línea de tierra.












Las dos vistas diédricas (en planta y alzado) quedarían de esta forma. Tras el giro las proyecciones diédricas del objeto quedan siempre correlativas.












Quitamos la referencia del contorno de los dos planos y tenemos ya la planta y alzado. La línea de tierra se representa en sistema diédrico por una recta que separa la planta del alzado y con dos segmentos en sus extremos.











Si la pieza tiene más complejidad puede ser necesario representar otra vista en algún plano más de proyección. En la figura vemos el plano del perfil (PP).














En la figura vemos en color amarillo lo que se proyecta en el plano vertical, en rojo y verde en el horizontal y en verde sobre el plano del perfil.
















En la planta se coloca la proyección ortogonal de la pieza “vista” desde arriba (en amarillo y azul claro). Correlativamente a la anterior aparece el alzado que es la vista frontal (naranja, verde y azul oscuro) y por último el perfil de la pieza (en rosa), como indica su denominación. Las partes no visibles de la pieza al observador según se coloca arriba para ver la planta, o de frente para ver el alzado aparecen discontinuas. Las líneas discontinuas son líneas que existen, que son intersección de superficies pero que no se pueden apreciar por estar detrás de alguna cara.















Una pieza con sus proyecciones en planta, alzado y perfil, y con una representación axonométrica de la misma.
La pieza, como tiene un hueco prismático cuyas aristas son tangentes a algunas caras de la figura, estas líneas aparecen con una disposición continua ya que son visibles.
















Vamos a representar en el sistema diédrico un prisma con otro prisma hueco en posición oblicua en su interior, para ello tenemos dos procedimientos:















Por un lado tenemos el sistema europeo en el que el observador se coloca encima de la pieza para verla desde arriba en planta. Se coloca detrás de la pieza para verla en el alzado o en el perfil. Con aproximación es lo que lo que se ve desde un punto de vista lejano para evitar la distorsión de las líneas concurrentes de la perspectiva, son proyecciones ortogonales del objeto sobre los tres planos de proyección.




















Una vez que se han proyectado las tres vistas sobre los tres planos de proyección, el plano de perfil se gira 90° hasta hacerlo coincidir con el plano del alzado. A continuación se giran los dos planos hasta hacerlos coincidir con el de la planta, coincidiendo todos con el plano del cuadro o del papel. El giro siempre se hace respecto a la línea de intersección de los planos.


















Tres vistas en planta alzado y perfil según el sistema europeo.




En el siguiente blog se explican las diferencias entre el sistema utilizado en Europa y el utilizado en América, llamados respectivamente diédrico en sistema europeo y diédrico en sistema americano:


https://diedrico-europeo-americano.blogspot.com/





























En la figura observamos una pieza en perspectiva axonométrica isométrica con sus tres proyecciones diédricas, planta, alzado, y perfil. Como muchas caras de la figura son coincidentes con otras o con la continuación de otras, de las vistas diédricas es difícil deducir la forma de la pieza.


Si representamos nuevas vistas y mostramos el interior de la pieza mediante líneas discontinuas facilitamos la comprensión de la misma. Tenemos no obstante el mismo problema que en el dibujo anterior, algunas aristas de la pieza son coincidentes por lo que tiene muy mala interpretación, ni siquiera la que muestra sus caras en distintos colores se aprecia con facilidad. Como la axonometría isométrica hace coincidir las aristas confundiendo la interpretación de la pieza, conviene hacer un giro de la misma en el espacio para obtener una nueva proyección axonométrico, como en el dibujo siguiente.



En esta vista resulta más fácil interpretar la pieza, no obstante como faltan líneas discontinuas no podemos interpretar bien las partes del dibujo no visibles según el punto de vista imaginario de la pieza (imaginario por cuanto la axonometría no tiene punto de vista, es una proyección ortogonal cilíndrica, de ahí que todas las aristas paralelas de la pieza salgan también paralelas en el dibujo, por esto se dice que el paralelismo es un invariante proyectivo en esta perspectiva).



En esta nueva proyección axonométrica trimétrica, podemos ya diferenciar con total nitidez los distintos elementos de la pieza. En consecuencia, cuando unas vistas diédricas no son suficientes para la interpretación del dibujo, -como tampoco lo serían en esta pieza diferentes cortes o vistas auxiliares de la misma-, tenemos que dibujar una perspectiva preferentemente axonométrica en la que las aristas de la pieza no sean coincidentes.













Cuadrantes en s. diédrico
A la izquierda podemos observar los cuatro cuadrantes del sistema diédrico. En el primer cuadrante un punto A tiene sus dos proyecciones ortogonales A1 A2 sobre el plano horizontal y vertical respectivamente. Al girar el plano vertical en sentido contrario a las agujas del reloj, la proyección A2 vertical del punto A queda sobre la línea de tierra mientras que la horizontal A1 queda por debajo de ésta, como se ve en el dibujo de la derecha.
En el segundo cuadrante B con sus dos proyecciones horizontal y vertical B1 B2, respectivamente, se transforman mediante el giro del plano vertical en B1 B2, ambas sobre la línea de tierra, como se observa en el dibujo de la derecha.
En el tercer cuadrante C, podemos observar que al girar el plano vertical, la proyección vertical del punto C2 pasa a estar por debajo de la línea de tierra mientras que la proyección sobre el plano horizontal C1 queda por encima de la línea de tierra, conforme al dibujo de la derecha.
Un punto D en el cuarto cuadrante con sus dos proyecciones horizontal y vertical D1 D2, respectivamente, tenemos que mediante el giro del plano vertical se transforman en 2 puntos alineados sobre una vertical por debajo de la línea de tierra, conforme aparecen el dibujo de la derecha.














Representación de elementos en sistema diédrico mediante coordenadas.
Tenemos los dos planos de proyección, el horizontal y vertical. La intersección de ambos planos o línea de tierra es considerada como el eje X (en color rojo). La línea perpendicular al eje sobre el plano horizontal por un punto cualquiera es considerado el eje Y (en color magenta). A partir de este punto u origen de coordenadas (0,0) hacemos una recta vertical y la consideramos el eje Z.
De esta forma representamos los puntos en los distintos cuadrantes: el punto A esta a 20 unidades del origen de coordenadas sobre el eje X., a partir de este punto hacia la derecha tiene un alejamiento de cinco unidades (tomado sobre el eje y) y una altura o cota de tres unidades (tomado sobre el eje Z), por tanto las coordenadas del punto A son (20,5, 3). En sentido contrario del que hemos utilizado tendríamos unidades con un valor negativo, por ejemplo, el punto B tiene por coordenadas (9, -7,4), esto quiere decir que sobre el eje X. está a nueve unidades, que a partir de este punto hacia la izquierda siguiendo el eje Y está a -7 unidades, y a partir de este punto a una altura o cota de cuatro unidades se localiza el punto B. Un punto que esté en el segundo cuadrante tiene sobre el eje y valor negativo y sobre el eje Z. su valor positivo, mientras que sobre el eje X. puede tenerlo positivo o negativo indistintamente.
El punto C del tercer cuadrante tiene las coordenadas negativas tanto del eje y como del eje Z., de esta forma el punto tiene por coordenadas (0, -8, -2), ello quiere decir que tiene por alejamiento ocho unidades y por cota o altura dos, negativos ambos por estar en el tercer cuadrante.
El punto D tiene por coordenadas (15,6, -20), en este cuadrante Z tiene siempre un valor negativo, mientras que el valor de Y es siempre positivo.













El sistema diédrico puede facilitar la comprensión del fundamento de los demás sistemas de representación.

En la figura tenemos un cubo que se proyecta de forma oblicua y mediante líneas paralelas sobre un plano llamado de cuadro PC. Una al menos de las caras del cubo es paralela al plano del cuadro.
Podemos observar que un segmento vertical de 10 cm se transforma en otro de 9 cm, esto quiere decir que la reducción que se aplica en este sistema de representación es de nueve decimos.
Tenemos también que a partir del eje X se empieza a contar un ángulo en el sentido de las agujas del reloj hasta orientar el eje Y. El ángulo que forman estos dos ejes es el ángulo de la perspectiva caballera, 315º en este caso.






En la figura podemos observar la representación diédrica de la perspectiva caballera, la proyección en planta y alzado de cada uno de los elementos mediante líneas paralelas que transforman la figura en planta en su perspectiva caballera.
Sobre la planta haremos la perspectiva caballera de la figura, que no es más que la sombra de la figura proyectada sobre el plano de la planta. Como vemos en el alzado la cara roja del cubo se transforma en el plano XY sobre la planta, mientras que la cara superior del cubo (en color verde) se transforma en la perspectiva en la cara verde.

http://perspectiva-caballera.blogspot.com/







En la figura podemos observar el fundamento del sistema axonométrico, tres ejes cartesianos, X Y Z se proyectan sobre un plano mediante líneas paralelas y de forma ortogonal al mismo. Estos tres ejes son la esquina de un cubo (forman entre sí dos a dos 90°, lo que en geometría se llama un triedro trirrectángulo).
Para obtener la verdadera medida del cubo que se proyecta de forma ortogonal sobre el plano del cuadro, se abaten las caras, de manera que podamos trabajar sobre el papel, sobre el plano del cuadro PC.
Sobre la cara abatida (x) (y) se colocan las vistas de la pieza y se proyectan ortogonalmente sobre la traza de la cara abatida hasta que cortan a los ejes x’ y’, obteniendo así la dimensión reducida sobre los mismos de las aristas del cubo.




En el dibujo tenemos la representación en sistema diédrico del triedro al que se ha abatido una cara, el abatimiento lo observamos en el alzado mediante el giro de la cara xy. Sobre la cara abatida (x) (y) se coloca una de las caras de la figura y se proyecta mediante ortogonales a la charnela hasta que intercepta a los ejes xy.
Al proyectar la forma plana tenemos que los vértices de esta inciden sobre los ejes de la axonometría xy, con lo que tenemos ya la perspectiva de la cara de la figura con su reducción correspondiente y en perspectiva axonométrica.

http://perspectiva-axonometrica.blogspot.com/









En la figura tenemos el fundamento de la perspectiva cónica, por el punto de vista V se hacen paralelas a la dirección de las aristas de la pieza V-F1, V-F2, hasta que interceptan en el plano del cuadro a los puntos de fuga F1 F2. Los lados n de la proyección de la pieza sobre el plano de la base se prolongan hasta que cortan al plano del cuadro, obteniendo las trazas tn que unimos con los puntos de fuga F1. La intersección de estas líneas es el cuadrilátero en perspectiva en color amarillo sobre el plano del cuadro. Como ejemplo tenemos que la perspectiva de n es d.
Para obtener las alturas de la pieza se colocan a partir de la traza tn las dimensiones verticales e s en verdadera magnitud y las proyectamos o d hacia los puntos de fuga F1 obteniendo la perspectiva de estas líneas verticales. Como podemos observar cada punto de la pieza U y su perspectiva U’ están alineados con el punto de vista V, y este es el fundamento de la perspectiva cónica.



En la figura tenemos la representación en sistema diédrico de la perspectiva cónica con sus dos proyecciones solapadas. Como vemos en planta sobre el cuadrado verde se prolongan sus lados n hasta que cortan al plano del cuadro en las trazas tn, puntos que subimos al alzado sobre la línea de tierra. Por el punto de vista V se hacen líneas paralelas a los lados de la figura en la base obteniendo en la intersección con el plano del cuadro en planta los puntos de fuga F1 F2. Estos puntos de fuga en planta se proyectan sobre el alzado sobre la línea que queda a la altura del punto de vista, que es la línea del horizonte F1 F2.
Uniendo los puntos de fuga con las trazas de la pieza tn-F1 tenemos la perspectiva del cuadrado verde sobre el alzado, que es el cuadrado amarillo. A partir de una de las trazas de estas líneas tn se colocan las medidas verticales e s de los elementos a representar. Estas dos medidas se proyectan hasta el punto de fuga F1 y donde interceptan a la vertical de cada punto q de la perspectiva del cuadrilátero amarillo tenemos la perspectiva cónica de la figura con sus dimensiones verticales en perspectiva. Podemos observar en la perspectiva que la proyección del punto de vista sobre la línea del horizonte, que llamamos punto principal, es tal que alinea
cada punto con su perspectiva, por ejemplo se puede observar que un vértice de la figura en el alzado U y su perspectiva U’ están alineados con la proyección del punto de vista V’ sobre el plano del cuadro en el alzado

http://la-perspectiva-conica.blogspot.com/


Proyección central en movimiento y por pasos:

Obtención de los parámetros de un objeto a partir de su perspectiva:

Perspectiva cónica en movimiento y por pasos:

Perspectiva de cuadro semiesférico:













En la figura podemos observar el fundamento de la perspectiva cónica para una figura con un plano del cuadro oblicuo respecto a las tres caras de la misma.
Por el punto de vista se hacen rectas paralelas a cada una de las aristas de la figura hasta que interceptan al plano del cuadro en los puntos de fuga F M L. Alineando el punto de vista V con cada uno de los vértices de la figura Y tenemos en la intersección con el mismo la perspectiva de cada uno de los puntos Y’.



En la figura podemos observar la representación en planta, alzado y perfil de la figura anterior. Como el plano del cuadro coincide con el plano del dibujo en vez de inclinar éste hemos inclinado el plano de la base y la figura, que tiene al menos una de sus caras paralelas al mismo. Como observamos en la planta y en el perfil, alineamos el punto de vista con cada uno de los puntos de la figura y en la intersección con el plano del cuadro hacemos proyecciones ortogonales al mismo. Por ejemplo, en el perfil alineando el punto Y3 con el punto de vista V3 tenemos J3, y en la planta alineando su correspondiente Y1 con el punto de vista V1 obtenemos J1. La intersección de las ortogonales en planta y en el alzado por esto puntos de intersección Y1 J3 nos determinan la perspectiva de la figura en el alzado J2, de igual forma procedemos con los demás puntos de la figura. Podemos comprobar que esta perspectiva es cierta, que es la figura tal y como la ve un sujeto desde el punto de vista V1 colocado a esa distancia en planta respecto al plano del cuadro PC, si prolongamos las aristas de la figura en perspectiva observamos que se cortan en tres puntos de fuga F2 L2 M2 que coinciden sobre la intersección de las ortogonales que pasan por los puntos de fuga. Como ejemplo obtenemos L2 de la intersección de las ortogonales por los puntos L1 L3 en la planta y en el perfil. También podemos observar que el punto de vista proyectado sobre el plano del cuadro en el alzado, que es el punto principal P2, está alineado con cada punto de la figura y su perspectiva, como ejemplo los puntos Y2-J2-P2 están alineados.

http://perspectiva-de-cuadro-inclinado.blogspot.com/
Publicado por en No hay comentarios:

Figuras, formas geométricas y desarrollos.

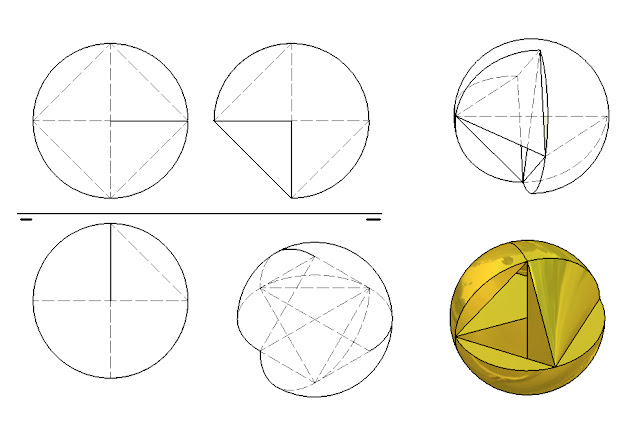
En la figura observamos una forma de construir esferas tangentes en el espacio. Los centros de las esferas son los vértices de un poliedro regular y sus radios corresponden a la mitad de cada arista del poliedro. Como el poliedro regular tiene todas las caras iguales tenemos que todas las esferas tienen el mismo diámetro y al mismo tiempo son tangentes en el punto medio de cada arista. En la figura observamos un icosaedro regular en planta, alzado y perfil. En cada vértice del icosaedro se ha dibujado una esfera tomando como radio la mitad de la arista con lo que todas las esferas son
iguales y tangentes entre sí.


VÍDEOS DE DIBUJO TÉCNICO Y GEOMETRÍA CLASIFICADOS POR TEMAS
Videos del sistema diédrico: http://videos-de-dibujo-tecnico-y-geometria.blogspot.com.es/2014/04/sistema-diedrico.html







Si el poliedro es arquimediano y por tanto está formado por polígonos regulares distintos aunque también regulares (de lados iguales), las esferas tendrán también el mismo tamaño aunque permanecerán tangentes entre sí, manteniendo una distancia mayor entre ellas por ser unas caras mayores que otras como se puede observar en este icosidodecaedro dado en planta y alzado.
Para dibujar ejercicios de esferas tangentes cuyos centros están en un mismo plano basta con hacer un ejercicio de circunferencias tangentes en el plano y darle volumen a las mismas.
http://tangencias-inversion.blogspot.com/
http://tangencias-potencia.blogspot.com/
http://tangencias-y-enlaces.blogspot.com/
http://teoremas-de-geometria.blogspot.com/2012/03/teoremas-de-arbelos.html









El teorema del cateto se representa en la planta de forma gráfica, y viene a decir que el rectángulo amarillo y el cuadrado azul son equivalentes que quiere decir que tienen la misma área (http://figuras-equivalentes.blogspot.com/).
Representamos el teorema del cateto en planta y en el alzado le damos la misma altura a los dos prismas. Como tienen igual área en la base, al tener la misma altura tienen el mismo volumen, de esta forma hemos calculado un cubo que tiene el mismo volumen que un prisma. Podemos coger los teoremas de equivalencias para calcular figuras equivalentes y hacer sus figuras correspondientes en tres dimensiones, esto es, con volumen.
















Al igual que se hizo con las figuras equivalentes, podemos seguir el mismo procedimiento para hacer figuras proporcionales en el espacio -esto es, que tienen la misma forma pero distinto tamaño (http://proporcion-escala-semejanza-homotecia.blogspot.com/).
Construimos dos figuras homotéticas (homólogas de eje impropio), que quiere decir que son proporcionales y al mismo tiempo que tienen sus vértices alineados con un centro de proyección O. La construcción de las figuras homotéticas las hacemos en la planta y en el alzado dibujamos sus correspondientes proyecciones verticales de manera que las dos alturas de los prismas estén también alineadas con el centro de proyección O. Como todos los segmentos o aristas de los prismas están alineados en sus vértices con el centro de proyección O, esto quiere decir que las figuras son iguales de forma aunque de distinto tamaño, esto es, homotéticas en el espacio.







El sistema diédrico es el más adecuado de los sistemas de representación para dibujar las acotaciones (medidas) de las piezas, ya que nos muestra caras en verdadera forma (con dimensiones reales o a escala) que no aparecen distorsionadas por el efecto de la perspectiva. Hay una normativa básica que debemos seguir para poder entender los dibujos: http://acotacion-normalizada.blogspot.com/.


http://secciones-cortes-roturas.blogspot.com/















El cálculo de sombras y de reflejos en el sistema diédrico facilita en gran medida la comprensión de los dibujos: http://calculo-de-sombras.blogspot.com/,
http://calculo-de-reflejos.blogspot.com/
http://sombras-en-perspectiva-conica.blogspot.com/





















Esferificar un poliedro (un dodecaedro regular), es proyectar sus aristas sobre la esfera al tiempo 
que los vértices del poliedro inciden en la esfera.
 De esta manera todas las aristas del poliedro se convierten en segmentos de círculos máximos 
ya que para proyectar la arista sobre la esfera se toma como centro de proyección el centro de la 
esfera, eso quiere decir que tendremos que hacer una circunferencia mayor cuyo centro es el de la
esfera y cuyo par de puntos de la circunferencia que cogemos son los extremos de ese segmento
o arista del poliedro, realmente esa arista corta a la esfera en los vértices y por esos dos puntos
pasará el arco que es un fragmento de la circunferencia mayor y que pasa por los dos extremos
de la arista y por el centro de la esfera
En sistema diédrico las proyecciones de las circunferencias mayores de esa esfera se
transforman por regla general en elipses salvo que la circunferencia mayor sea paralela 
al plano de proyección,  en ese caso se transformara en una circunferencia, mientras que 
en el caso de que las circunferencias mayores sean perpendiculares al plano de proyección, 
se transformaran en líneas rectas.








Pieza representada en planta, alzado y perfil con vista auxiliar y representación en perspectiva axonométrica isométrica.
Modos de dibujar en axonometría:
http://perspectiva-axonometrica.blogspot.com/
http://perspectiva-caballera.blogspot.com/


















Aquí podemos observar la sombra arrojada sobre el suelo que produce un rectángulo rojo a y un objeto formado por dos prismas paralelepípedos con sus sombras propias y arrojadas, ambos objetos son iluminados por el sol, que está en la dirección d y forma un ángulo h llamado altitud respecto al plano horizontal, determinado por su dirección d y por su proyección ortogonal d1 sobre el plano horizontal.
Otra parámetro que determina la localización del sol es el ángulo g que forma la línea norte-sur respecto al plano vertical que contiene al rayo solar d, a este ángulo se le llama acimut y se cuenta en el sentido de las agujas del reloj.
Como podemos observar en el dibujo, la proyección ortogonal de un rayo solar d1 sobre el plano horizontal del suelo, es la dirección que siguen las sombras de las líneas verticales de los prismas, en el dibujo señalado con la letra m. Mientras que la dirección de cualquier rayo solar d se proyecta en el alzado según la dirección n que es la dirección de la sombra arrojada de un segmento perpendicular al plano vertical.





En el dibujo observamos en el sistema diédrico los elementos de la escena anterior. Como podemos observar en el dibujo, el sol está tan alejado que los rayos se consideran paralelos, por lo que líneas paralelas del prisma generan sombras paralelas, las sombras de las líneas verticales son todas paralelas a la dirección de la sombra arrojada as.
El rayo solar queda definido como cualquier recta en sistema diédrico, por su dirección d1 en planta, y su dirección d2 en el alzado. El prisma doble con sus sombras propias y arrojadas y el cuadrilátero paralelogramo a de color rojo con su sombra as sobre el plano horizontal.
La línea norte-sur NS determina con la sombra arrojada as del cuadrilátero, el ángulo g llamado acimut, que se cuenta a partir de la línea norte-sur hacia la derecha o en el sentido de las agujas del reloj.
La altitud h aparece en color azul, y es el ángulo que forma la proyección ortogonal del rayo solar sobre el suelo, esto es, la sombra as sobre el plano horizontal, y el rayo solar d1. Como el plano que contiene a estas dos líneas es vertical necesitamos abatirlo para tener su verdadera magnitud. Al abatirlo obtenemos (d1), el ángulo entre esta línea y d1 es la altitud h del sol y aparece en verdadera forma en planta tras su abatimiento.
De esta manera en la planta tenemos determinada la posición exacta del sol, el ángulo g que forma su dirección respecto a la línea norte-sur en color verde (acimut), y el ángulo h que define su dirección respecto al plano horizontal y en color azul (altitud).
















Observamos un reloj de sol y su construcción. Una varilla llamada gnomom proyecta la sombra sobre un plano amarillo o plano del cuadrante, en este caso horizontal. Un plano azul llamado s, es perpendicular a la varilla y describe la trayectoria del sol en una circunferencia completa, esto quiere decir que los 360° que cubre se divide entre las 24 horas del día de lo que resulta que el ángulo entre las rectas de la radiación sobre el plano azul es de 15°. Donde estas rectas cortan al plano amarillo, se unen con el punto de intersección de la varilla con el plano amarillo del cuadrante. Tenemos entonces que la sombra de la varilla es cada una de las líneas de color rosa que están sobre el plano amarillo. Teniendo en cuenta que en la línea norte-sur el sol proyecta la sombra de la varilla a las 12 de la mañana sobre el plano amarillo, a la derecha 15° tenemos la sombra de las 13 horas, la segunda varilla a 30° respecto a la línea norte-sur tenemos las 14 horas, la tercera varilla a las 15 horas, la cuarta varilla a las 16 horas, etcétera.
La posibilidad de dibujar en el sistema diédrico la figura nos facilita su fácil comprensión y construcción, ya que solo hay que tener en cuenta que sobre el plano azul todas las rectas que cortan a la varilla forman entre sí 15° y que el ángulo que forma la varilla con el plano amarillo es exactamente el de la latitud del lugar donde se pone el reloj de sol, ya que se demuestra en geometría que para que el sol proyecte de igual forma las horas en ángulos iguales, la varilla tiene que ser paralela al eje terrestre de rotación y esto supone que el ángulo entre la varilla y el plano horizontal o cuadrante horizontal en este caso, sea igual al ángulo entre el plano del Ecuador terrestre y el punto de lugar donde se ubica el reloj que no es otra cosa que la latitud.

Un ejemplo para un reloj de Navarra, con latitud 42º: La sombra de la aguja violeta, (situada sobre un plano vertical imaginario por la linea NSur), sobre las líneas verdes determina las horas.














Como podemos observar en el perfil de la esfera terrestre estamos situados en la latitud norte a 40° definido el ángulo a partir del Ecuador.
El cuadrante del reloj es un plano horizontal que se apoya en el punto P, nuestra localización. Como podemos observar en el dibujo, los 90° que forman el eje terrestre y el Ecuador menos la latitud es igual al ángulo amarillo.
En nuestro reloj de sol, la vertical y el cuadrante forman 90° por lo que siendo el gnomon una recta paralela al eje terrestre tenemos que el gnomon forma con la vertical el mismo ángulo amarillo que la vertical con el eje terrestre, de lo que se desprende que la latitud (90º menos el ángulo amarillo) es igual al ángulo que forma el gnomon y el cuadrante (90º menos el ángulo amarillo).


http://reloj-de-sol.blogspot.com/
http://cartografia-celeste.blogspot.com/


http://los-angulos-en-la-circunferencia.blogspot.com/










En la figura observamos distintas formas de representar la perspectiva de un objeto, una proyección cilíndrica ortogonal o axonométrica en la que las paralelas de la figura se mantienen invariables y una perspectiva lineal, central o cónica (semejante a la que aprecia nuestra vista) en la que las paralelas siempre tienen un punto en común, llamado de fuga.




http://proyeccion-central-dinamica.blogspot.com.es/
http://perspectiva-conica-dinamica.blogspot.com.es/











Si las verticales se cortan en otro punto común tenemos que la perspectiva es de plano inclinado. http://perspectiva-de-cuadro-inclinado.blogspot.com/
Si a parte del punto común o fuga de las verticales (por la parte inferior en este caso) tenemos otra fuga común para estas líneas por la parte superior tenemos una nueva perspectiva no euclídea llamada curvilínea:












Intersección de tres astroides extruidos - en la zona izquierda en rojo-, en las direcciones de los ejes cartesianos.

En color verde intersección de dos astroides extruidos en dos direcciones de ejes cartesianos.







En la figura observamos un icosaedro y un dodecaedro en planta y alzado. Como podemos observar ambos están inscritos en un cubo y sus aristas a b están centradas en el centro de cada cara del cubo. Si sumamos la arista del dodecaedro a la arista del icosaedro b comprobamos que son del tamaño de la arista del cubo d. Podemos comprobar también que la arista del cubo es a la arista del icosaedro como la arista del icosaedro es a la arista del dodecaedro, por lo que tenemos que las tres medidas están en proporción áurea d/b=b/a, una relación mágica entre dos segmentos cuyo cociente es 1,618 y que aparece de forma continua y necesaria en el orden de la naturaleza. Además en las dos proyecciones en alzado de las figuras la arista del icosaedro es igual a la diagonal de cada cara pentagonal del dodecaedro, ya que en todo pentágono regular el lado y su diagonal están en proporción áurea.
http://la-proporcion-aurea.blogspot.com/
http://dodecaedro-en-icosaedro.blogspot.com.es/







Figura formada por un prisma en forma de cuña en el que se ha introducido otro prisma de base rómbica respetando el hueco que produce en su desplazamiento.




















Un octaedro regular es un poliedro regular formado por ocho caras que son triángulos equiláteros. Un triángulo equilátero es un polígono regular, esto es, el que tiene los lados y ángulos iguales
(http://poligonos-regulares.blogspot.com/).
El octaedro se puede construir uniendo dos pirámides unidas por sus bases cuadradas.
Las tres diagonales del poliedro tienen el mismo tamaño de ahí que tanto la proyección en planta como la proyección A sean cuadrados. La proyección de una cara en verdadera magnitud como la que corresponde a la vista auxiliar B genera como contorno de la figura un hexágono regular.











Un tetraedro regular es un poliedro regular formado por cuatro caras que son triángulos equiláteros. Tenemos en la sección paralela a una cara A-A que al desplazar el plano siempre paralelo a la misma se va transformando en un triángulo equilátero cada vez más pequeño que llega a convertirse en un punto. Una posible vista de la figura tiene por planta un cuadrado B -es la vista auxiliar perpendicular a una de las aristas de la figura- ya que las diagonales que se cruzan ortogonalmente forman entre sí 90° y son de igual tamaño.











Esta superficie se genera por la evolución de una circunferencia que se va transformando en una elipse, por esto se denomina superficie de evolución. Es también una superficie reglada alabeada ya que podemos unir mediante rectas sus dos bases, la circunferencia y la elipse. Si al prolongar las generatrices que unen las dos curvas tenemos una recta, la superficie es un conoide, de ahí que podemos decir que es un conoide truncado.





En la figura vemos la intersección de dos cilindros 
Cuando seccionamos por la mitad esas dos figuras que se penetran a 90 grados.se provoca una bóveda esquifada
 En el caso que nos ocupa los dos cilindros tienen ejes concurrentes y sus secciones circulares son iguales, la interferencia de ambos cilindros provoca esta forma curiosa qué se puede ver en el dibujo


Bóveda vaída
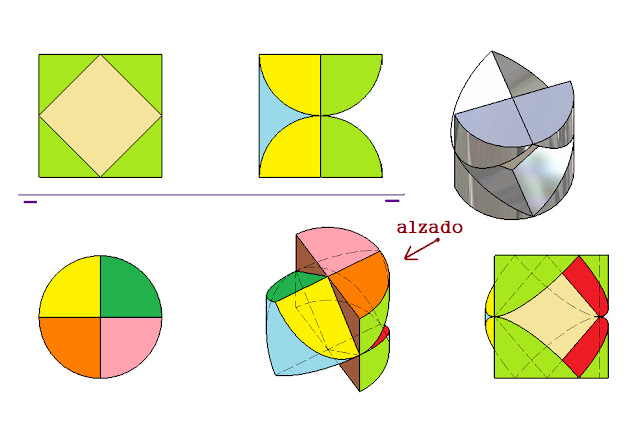
Una bóveda vaida es una semiesfera en cuya circunferencia base se inscribe un cuadrado y por ese 
cuadrado se levantan 4 planos verticales que cortan a la semiesfera.
La región que acota  esos cuatro planos es una bóveda vaida y si hacemos la simétrica respecto
a la circunferencia base obtenemos la unión de dos bovedas vaidas por la base, o lo que es lo mismo.
una esfera cortada por 4 planos extruidos a partir de un  cuadrado inscrito en un círculo máximo
de la misma.








Una superficie reglada alabeada se puede obtener mediante rectas que unen dos curvas como la figura. La figura está formada por la unión de rectas entre dos directrices de distinto sentido de distintas alturas. Como se tiene que las rectas que forman la superficie son siempre paralelas al plano del perfil de proyección y además se está uniendo una circunferencia con una recta que pasa por la mitad de la figura, tenemos que la superficie está formada por dos semi-conoides.















Un prisma al que se le ha restado un cilindro interior que pasa por el eje.






















Una esfera que se le ha restado un cono y un prisma en forma de cuña.





















Cono con hueco en forma de toro.
























Un hiperboloide de una hoja con sus posibles secciones cónicas.
El hiperboloide de una hoja está engendrado por una hipérbola que gira en torno a un eje. La suavidad de esta curva cónica hace que se utilice en elementos de diseño aerodinámico como en coches, barcos, aviones, etc.
















Figura simétrica formada por dos conos unidos por su base en los que se ha practicado un hueco con otros dos conos invertidos. La figura se puede engendrar por la revolución de un cuadrado que gira en torno a un eje de manera que su diagonal es perpendicular al mismo.
















Intersección de un prisma cuya base es un rombo, con una superficie esférica y otra cilíndrica enlazadas y en las que se ha practicado dos huecos esféricos.


























Helizoide recto. Superficie que genera una recta que ortogonalmente a un eje gira y al mismo tiempo se desplaza a través de él, manteniéndose siempre ortogonal.

http://helicoides.blogspot.com/

















Esfera con un cilindro, semiesfera y un prisma huecos en su interior.



























Un prisma en el que se ha practicado el empalme de sus vértices y aristas, aplicando en los mismos esferas y cilindros respectivamente. La norma permite para este tipo de superficies hacer líneas finas en la unión de las superficies tangentes para definir mejor las formas. En el interior se ha practicado un hueco que se transforma de rectángulo en circunferencia, por lo que es una superficie de evolución que va transformando el rectángulo en otro al que se le va redondeando los vértices hasta convertirse en una circunferencia.


















Figura formada por cuatro piezas con un cilindro hueco que la atraviesa.

























Figura formada por cuatro piezas. Está construida por la intersección de una esfera y un prisma cuyo eje pasa por su centro y a la que se le ha restado otro prisma interior.
























Prisma al que se le ha restado otro prisma y un cilindro.

















Figura formada por un cuarto de esfera y dos cilindros, además de un hueco cilíndrico aplicado sobre uno de los cilindros. Se ponen primero las tres vistas para poder obtener la perspectiva axonométrica a partir de ellas.








En el alzado podemos observar el plano de corte AA que define el rayado del perfil. 









Cubo con un hueco esférico centrado en su interior. En la figura en planta en color rojo podemos ver un corte de la figura que se puede ver en detalle en el alzado (AA), dejando ver 3/4 de la figura, tal y como aparece en la perspectiva que aparece al lado del alzado. Como podemos observar el corte aparece con dos ejes que forman entre sí 90°, tal y como se ve en la planta.








En la figura podemos observar cilindros y esferas en positivo y en negativo, entendiendo si son volúmenes o huecos, respectivamente. Se muestra también una vista a auxiliar en la que se aprecia el hueco cilíndrico menor con su circunferencia en verdadera forma.






En la figura podemos observar una pieza en dos vistas en planta y alzado. En la planta se aplica un corte para poder observar la sección A-A, la circunferencia en verdadera forma y magnitud, mientras que en el alzado se aplica otro corte para poder acotar la profundidad del cilindro (6), ya que pese a ser un detalle que se ve en la planta, por ser discontinuo, no está permitido acotar.
En el corte que se practica en la planta observamos que los dos planos de corte forman un ángulo entre sí, el detalle que aparece cortado A-A (3:1) tiene las dimensiones reales en la sección, de lo que se desprende que los dos planos de corte de la figura han sido girados para obtener la nueva proyección A-A.





Superficie de revolución acotada






En la figura podemos ver la planta y alzado de una pieza que aparece más abajo en perspectiva.











Figura formada por un prisma con varios prismas huecos además de un hueco cilíndrico enlazado con otro esférico.











Esfera dividida en ocho partes iguales a la que se le ha quitado cuatro de sus partes.
La esfera de metal refleja el entorno, una perspectiva que es posible calcular mediante el cálculo de reflejos.




























Esfera con un hexaedro hueco en su interior (poliedro de 6 caras) al que se le han extruido las caras.
http://geometria-de-la-esfera.blogspot.com/





http://proyeccion-estereografica.blogspot.com/























Figura formada por la intersección de tres cilindros de ejes ortogonales entre sí y a la que se le ha practicado un hueco en forma de prisma.























Trapecio extruido con dos huecos cilíndricos.




























Figura formada por la intersección de tres cilindros de ejes ortogonales entre sí. La figura esta proyectada en planta, alzado y perfil y contiene una vista auxiliar.





















Plancha en forma de paraboloide hiperbólico.



















Paraboloide hiperbólico con sus tres proyecciones: en planta y perfil un triángulo y en el alzado un trapecio.





























Como se ve en la figura el paraboloide hiperbólico se puede engendrar por una línea que al tiempo que gira se desplaza en una dirección distinta del plano que la contiene -en vez de una recta se ha cogido un rectángulo para que la figura tuviera volumen. En la planta observamos la figura de un rectángulo, la base que se desplaza a cierta altura al tiempo que gira, con lo que engendra la superficie de este paraboloide hiperbólico con grosor.




















Un octaedro regular al que se le ha practicado un hueco cilíndrico.




























Un muelle engendrado por una esfera que se desplaza siguiendo un helicoide es un serpentín. El helicoide se engendra por un punto que se mueve en una circunferencia que al mismo tiempo se traslada por un eje perpendicular a su centro.

En la siguiente página podemos observar la transformación cilíndrica a esférica de un serpentín y otras transformaciones:

http://poliedroestrellado.blogspot.com/























Un icosidodecaedro es un poliedro arquimediano que se puede obtener al cortar el dodecaedro regular o el icosaedro regular. Como todo poliedro arquimediano está formado por polígonos regulares aunque no todos iguales. En la figura se observan dos secciones del poliedro, en una de ellas, en corte que determina CC, el plano pasa por los vértices de los cincos triángulos equiláteros, por lo que se obtiene un pentágono regular.


















Un icosaedro regular es un poliedro regular, por lo tanto tiene todas las caras iguales, siendo éstas polígonos regulares. Tiene por caras 20 triángulos equiláteros y es un poliedro dual del dodecaedro, ello quiere decir que si cogemos los puntos medios de cada cara y los unimos obtendremos el dodecaedro regular, de igual forma si cogemos los puntos medios del dodecaedro regular obtenemos el icosaedro regular.















Esta figura es un poliedro arquimediano que se engendra al achaflanar los vértices y aristas del icosaedro regular. En la sección AA se muestra el interior de la figura, el hecho de que se puedan ver las caras quiere decir que el objeto es una superficie y no un sólido, o sea que es hueco.


























Dodecaedro regular con sus caras coloreadas para una mejor comprensión de la pieza. Como se puede ver en los colores, de una proyección a otra sólo coincide una única cara, esto quiere decir que de las cuatro caras que tenemos en planta, sólo una se ve en el alzado: la amarilla. De las cuatro del alzado sólo se ve uno en el perfil, la rosa.






















Cono al que se le ha quitado una superficie cilíndrica y otra en forma de toro. Como la penetración de estas dos últimas figuras se hace de forma tangencial, las curvas alabeadas que se producen tienen forma de ocho, y están adecuados al mismo tiempo la superficie cónica, ya que son curvas de intersección de ambas superficies.

















Cono en planta y alzado con tres posibles secciones cónicas del mismo: cuando el plano cortante es paralelo dos generatrices, tenemos la hipérbola, cuando es paralelo a una generatriz tenemos la parábola y cuando no es paralelo a ninguna tenemos la elipse.



























Cuando el plano que corta el cono se va girando produce las distintas secciones cónicas, en el caso de que el plano de corte se desplace y llegue a ser tangente al cono en una generatriz, la curva cónica se transforma en una recta a la que se le llama cónica degenerada. Otra cónica degenerada es cuando el plano de corte pasa por el vértice produciendo dos nuevas posibles figuras, dos rectas que cortan al cono y pasan por el vértice del mismo o bien que el plano pase por el vértice sin cortar a la superficie con lo que la cónica degenerada es un punto.

















Esfera con un hueco prismático de base triangular equilátera.


























Figura de evolución que transforma una circunferencia en un cuadrado de forma progresiva. Una sección a cierta altura engendra una curva entre el cuadrado y el círculo, según nos acercamos al cuadrado, los arcos de circunferencia de la nueva figura tienen su centro cada vez más alejado. En el momento en que sea un cuadrado, los centros de las circunferencias de los lados de la figura estarán en el infinito.















Posibles secciones de una plancha con forma de paraboloide hiperbólico, observamos que cuando el plano cortante BB contiene una generatriz y es paralelo a un plano director, la sección es una línea recta.

























El paraboloide elíptico es una superficie de revolución engendrada por una parábola que gira en torno a su eje. Las posibles secciones del paraboloide son, como vemos en la figura una parábola, una elipse o una circunferencia.




















Para la construcción de los poliedros arquimedianos existen dos tipos de truncamiento de los poliedros regulares, aquel cuyo plano cortante pasa por la mitad de la arista -tipo1- o aquel truncamiento que pasa por un tercio aproximado de la arista -tipo2-, de forma que el polígono resultante sea regular, como en la figura.


















El icosaedro regular se puede construir con pirámides de bases pentagonales cuyos lados son triángulos equiláteros, de esta forma la sección F-F tenemos que es un pentágono. La misma forma aparece en la vista auxiliar que sigue la dirección D, en la que se proyecta otro pentágono regular. Por otro lado en la proyección obtenida en la dirección C, una cara de la figura aparece en verdadera forma y el contorno del poliedro es un hexágono regular, aunque la sección del mismo no produzca esta figura, ya que los lados de este hexágono regular no son coplanarios.














Un sólido en forma de cono al que se le ha practicado dos huecos esféricos. Como las esferas huecas son tangentes al cono dividen a este en tres partes. El plano de corte A-A que es tangente a las dos esferas genera una sección elíptica en la que los puntos de tangencia a las esferas son los focos de la elipse, según el teorema de Dandelin:
http://curvas-conicas.blogspot.com/
















El cilindro representado en planta y alzado con su perspectiva axonométrica isométrica. Si bien una circunferencia en perspectiva se transforma en una elipse, se puede sustituir ésta, por su parecido, por un óvalo en el que para hacer sus arcos hacemos centro sobre el vértice del cuadrilátero de la base. Para hacer el arco menor hacemos desde el centro anterior una recta perpendicular a uno de los lados del rombo, donde ésta recta corte al eje horizontal tenemos el centro del otro arco.














El cono en planta y alzado y su representación en perspectiva axonométrica isométrica. De igual forma para hacer la base se ha construido un óvalo con los centros que se marcan en la figura.
La elipse que ha sido sustituida es una curva más suave que el óvalo y no se nota en ella la diferente transición entre sus puntos como en los de enlace entre dos arcos del óvalo. Otra diferencia notable entre las dos figuras es que si dibujamos la elipse correspondiente al cuadrilátero en la que se inscribe el óvalo, la elipse aparece más afilada, más excéntrica, esto quiere decir que el eje mayor es de más dimensión que el del óvalo.


























Cono en planta y alzado apoyado sobre un plano proyectantes vertical. Para dibujar esta figura se debe partir primero del alzado del cono para proyectar a continuación sus puntos sobre la planta. En la planta el eje de la circunferencia se transformara en un eje menor de la elipse y vendrá dado por la intersección de la recta horizontal por donde pasa el vértice y la proyección de la base del cono del alzado. Mientras que el eje mayor se corresponde con el diámetro del cono del alzado, ya que en éste está en verdadera magnitud.











Para hacer los planos tangentes a un cono desde un punto exterior P, unimos ese punto con el vértice V del cono y tenemos la traza de la recta Ha en su prolongación. Desde esa traza se hacen las tangentes x1 g1 a la base del cono y los puntos de tangencia de la circunferencia se unen con el vértice del cono. Estas rectas de unión de los puntos de tangencia con el vértice del cono son las líneas tangentes de los planos al cono y los dos planos tangentes eran determinados por las rectas x1-a g1-a.














Superficie de revolución formada por dos conos y dos esferas. En la esfera exterior sólida contiene un cono hueco que asimismo contiene una esfera sólida tangente al mismo y dentro de esta segunda esfera otro cono invertido respecto al anterior.
Las dos esferas son sólidas mientras que los dos conos son huecos. Como el cono tiene su base tangente a la esfera, divide a la esfera en dos figuras.













La figura está formada por una esfera a la que se le ha restado un cilindro elíptico.






































































Un cubo es atravesado por dos conos cuyas bases son circunferencias tangentes a dos caras adyacentes del mismo. La intersección de los dos conos produce dos elipses, una elipse mayor X que es la que corresponde a la zona de interferencia de los dos conos y una elipse menor que está formada por dos partes, una correspondiente a la penetración de un cono en el otro y recíprocamente.
En el alzado se puede ver como la intersección correspondiente a la elipse mayor viene dada por la bisectriz m de los lados a b del cubo. Los extremos V H del eje de la elipse menor G corresponden a la zona comprendida entre estos puntos, que son la intersección de las generatrices contorno del cono (s-LK para el punto V, por ejemplo).









































La figura está formada por un cubo al que se le ha restado un cilindro en una dirección y un prisma en otra, ambas superficies radiadas tangentes en una generatriz.


Un cubo o hexaedro regular es un poliedro regular formado por seis caras cuadradas.
























La figura está formada por la composición de dos cubos por lo que es un poliedro compuesto:
http://poliedroscompuestos.blogspot.com/





Página de cortes en poliedros compuestos.























Un cubo al que se han redondeado sus vértices y aristas es atravesado por el centro de cada una de sus caras por tres cilindros del mismo diámetro.

























Un objeto de revolución con su tapa muestra en el alzado un corte parcial imaginario por lo que su superficie cortada aparece con un rayado a 45° representado mediante líneas paralelas y equidistantes. Como el objeto y la tapa son elementos distintos el rayado debe también ser distinto pero siempre a 45°, para diferenciarlos se puede variar la dirección del rayado o bien variar la distancia entre las líneas paralelas de el rayado. Gracias al semicorte se facilita que se pueda ver en el alzado el interior de la pieza en la mitad de la misma y el exterior en la otra mitad.
















En una semiesfera se ha practicado un hueco en forma de toro tangente a su superficie, por lo que la línea de contacto de ambas superficies aparece en la planta y es coincidente en el alzado con el contorno de la semiesfera, dividiendo a la semiesfera en dos partes.
















Una esfera ha sido agujereada por otra esfera interior que se ha desplazado en una dirección diametral recta de la esfera, generando una superficie hueca en forma de cápsula.
En la representación perspectiva aparece la mitad de la figura mostrando el interior de la misma.
















Esta figura está formada por la intersección de un cono y un toro. Al cono se le ha restado el toro generando el hueco que se puede percibir en la figura. La intersección se calcula de la manera usual: se pasan planos, por ejemplo horizontales, que corten a ambas figuras. La intersección de cada plano con las dos figuras nos determina dos curvas que en su intersección definen los puntos de intersección de las dos superficies.
Los planos horizontales cortan al cono según circunferencias, mientras que cortan al toro con curvas mucho más complejas, por lo que la resolución del ejercicio es algo complicada. Si cogemos planos ortogonales al eje de revolución del cono lo cortarán, por ser una superficie de revolución, según circunferencias paralelas de distinto diámetro y cortarán también al cono en curvas parabólicas, ya que el eje de revolución del toro es perpendicular a la generatriz del contorno del alzado del cono.











Esfera a la que se le ha quitado un prisma de base triangular.
































Prisma al que se le ha restado otro prisma.









































































Un cubo al que se le ha restado por cada una de sus caras otro prisma cuyas aristas son tangentes a sus caras. La intersección de los prismas en las tres direcciones genera esta figura tan curiosa.
































































En la figura podemos observar un cubo al que se le ha restado un cilindro colocado de forma oblicua respecto al mismo.



































































En un cubo se han practicado dos huecos cilíndricos, uno que está en el interior de la figura y otro cuyo eje coincide con una arista del cubo.
En la perspectiva se puede ver la intersección de los dos cilindros.









































































Un cubo es atravesado por un cilindro y un prisma, ambos tangentes al mismo. La intersección entre ambas figuras huecas provoca en el perfil arcos de circunferencia tangentes que son las proyecciones de las elipses de intersección de ambas superficies huecas.

































































Figura formada por un prisma de base triangular a la que se le ha restado porciones cilíndricas.














































































Esfera en la que se ha practicado un hueco interior formado por dos conos y un cilindro. En la proyección en perspectiva, los vértices de los conos coinciden con puntos de sus bases, de ahí que sólo aparezca representada una forma cilíndrica.

























































figura formada por un cilindro al que se le ha quitado otro cilindro.






















































































la figura está formada por un cubo al que se le ha restado dos toros tangentes en sus circunferencias a las caras del mismo. Los toros tienen su centro en el punto medio de las aristas opuestas del cubo. Como las circunferencias de los toros son tangentes a las caras del cubo, lo son también en el desplazamiento a las caras adyacentes por lo que dividen al cubo en tres partes.





















































figura formada por un prisma que se le han restado tres cilindros y otro prisma.

































































figura formada por una esfera a la que se le ha quitado por la parte superior otra esfera, generando una superficie de color naranja, y por la parte inferior un cilindro y un prisma, provocando la superficie de color azul.






















pieza industrial formada por enlaces de superficies cilíndricas y prismas, en el interior de la figura se han practicado varios huecos cilíndricos de diferente diámetro.




















la figura está formado por la unión de dos pirámides. Tiene por contorno en planta, alzado y perfil, un triángulo equilátero, otro, y un cuadrado, respectivamente.

































































en el interior de una esfera se ha dibujado un pentágono regular y se han girado respecto a un diámetro de la misma. La superficie interior que genera se vacía provocando que la esfera tenga un hueco con forma de toro de sección pentagonal regular.





















la figura está formada por un elipsoide,-figura formada por la rotación de una semielipse sobre su eje mayor en este caso-, al que se le ha restado un prisma pentagonal regular


























































figura formada por la intersección de prismas y cilindros.






























en la figura podemos observar corte AA por planos paralelos en el que sería variado su dirección para interceptar el hueco de la pieza. Igual que en los extremos del plano cortante se marcan líneas de mayor grosor, en el cambio de dirección del plano que corta la pieza también se hace lo mismo.

























un cilindro al que se le han practicado cuatro huecos cilíndricos y otro prismático en su parte superior.



























figura formada por un prisma al que se le han redondeado y torcido sus extremos.





























en la figura se han practicado un hueco cilíndrico y otro prismático, en este último se ha practicado un agujero que se muestra en alzado en detalle mediante un corte parcial.



























pieza industrial representada en sistema diédrico con una vista auxiliar y dos proyecciones ortogonales en perspectiva.






















cilindro al que se ha restado un prisma y tres huecos cilíndricos, a parte de sus vistas diédricas se ha representado un corte del mismo y su representación en perspectiva.





















En la figura tenemos una superficie de revolución engendrada por un trapecio que se ha girado en torno a un eje al que se le ha redondeado un borde inferior.
En la cara superior de la superficie se han practicado mediante una matriz polar, cilindros concéntricos tangentes al contorno de las circunferencias de la corona circular.


















figura formada por un prisma y la interferencia de varios cilindros.


















3/4 de cilindro con 2 cilindros huecos









Podemos observar un prisma hexagonal con un hueco esférico en cuyo eje central inciden tres prismas hexagonales en una disposición polar cuyas bases tienen sus vértices tangentes a las circunferencias huecas de las caras del prisma que genera la esfera interior.
Podemos observar en la sección del plano vertical por los puntos BB la parte visible de la superficie esférica en color verde y los prismas en color morado y azul. El corte permite ver siempre lo que está detrás del plano de corte.



















Figura compuesta por intersección de formas extrusionadas en forma de arcos equidistantes.









































































En la figura se puede observar una esfera hueca con tres cilindros huecos interiores con tres bases distintas. Podemos observar en detalle a una escala mayor, esta escala es la que corresponde a la pieza en la realidad, no al dibujo en la planta y en el alzado, esto quiere decir que el detalle es seis veces más grande en el dibujo que en la realidad. En el alzado de la figura se representa un corte de la misma coincidente con el eje de simetría horizontal de la pieza. Como este corte corresponde a un plano que pasa por el centro y coincide con un eje de simetría, no se indican los detalles normalizados del corte, ni las letras que pasan por el plano vertical de corte.


















En la figura observamos un cono al que se le han restado otros dos conos, un cono hueco cuyo eje es perpendicular al cono mayor y otro cono cuyo eje es paralelo al mismo. La intersección del cono mayor con los otros dos genera dos curvas alabeadas, esto es, curvas cuyos puntos no pueden incidir todos sobre un plano.



















En la figura observamos la importancia de los cortes a la hora de representar las piezas. El plano vertical que pasa por los puntos BB define con total precisión el corte del detalle en el que se pueden ver las circunferencias concéntricas de las superficies cilíndricas de la figura. Mientras que el plano horizontal determinado por los puntos AA, define con total precisión el ángulo que forma la dirección de los ejes de los cilindros respecto a la estructura de la pieza.

















En la figura podemos observar una esfera con dos huecos cilíndricos y dos huecos prismáticos. Al mismo tiempo se le ha quitado un cuarto de la esfera, dejando ver con más claridad el interior de los cuatro huecos interiores comunicados.

































































En la figura podemos observar un hexaedro (figura formada por seis caras, en este caso dos pirámides unidas por la base) con dos huecos esféricos, uno de ellos intercepta dos caras y a la otra esfera. El otro hueco esférico intercepta a la esfera anterior cortándola según una circunferencia. La esfera intercepta además a cuatro caras de la figura, cortándolas según cuatro circunferencias.
Es una pieza difícil de intuir, sobre todo en su proyección en el perfil, en el que una de las circunferencias que genera la esfera interior sobre una de las caras coincide con una de las caras que se transforma en una línea recta sobre esta proyección, de ahí que no se pueda ver la circunferencia ya que coincide con la cara en una misma línea.
La vista auxiliar A permite ver las circunferencias coincidentes que dejan ver el fondo en color blanco.















En la figura podemos observar la composición de una figura generada con cilindros prismas y conos.






















prisma con dos huecos cilíndricos y sus intersecciones respectivas.
































cilindro en el que se han practicado dos huecos, uno cilíndrico y otro prismático de base hexagonal.





























prisma con dos huecos, uno cilíndrico en color azul y otro cónico en color amarillo, con su intersección respectiva.






















hiperboloide reglado con un hueco prismático hexagonal y con su parte superior redondeada.
























figura formada por enlace de prismas y cilindros.

























prisma al que se le ha realizado una torsión de su cara superior generando superficies curvas en sus laterales con forma de paraboloides hiperbólicos.























en la figura podemos observar un poliedro al que se le ha restado una esfera. Como el centro de la esfera no pasa por el centro del poliedro sino que está desplazado, tenemos que corta a las caras en circunferencias mayores por uno de los lados.


















porción de cilindro al que se le han restado dos prismas.









































































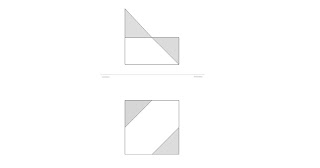
prisma formado por la unión de otros dos (en color azul y verde sus caras verticales), y que se ha cortado por dos planos oblicuos generando las caras de color amarillo y naranja.
























cilindro en el que se han practicado dos huecos cilíndricos y otro prismático.


























pieza en cuya representación en perspectiva se ha hecho un corte imaginario quitando un cuarto de la misma.















Cilindro con hueco esférico









pieza constituida por la intersección de cuatro cilindros y un hueco prismático.
























sólido prismático al que se le han empalmado vértices y aristas y en el que se ha practicado un hueco de media cápsula y otro cilíndrico.





















prisma formado por la diferencia de dos huecos y su intersección respectiva, uno cilíndrico de color rosa y otro cónico de color amarillo.



























elipsoide con un hueco esférico centrado en su interior.
























cubo en el que se han practicado dos huecos con forma de prisma hexagonal.




























prisma en el que se ha practicado un hueco de sección hexagonal regular.























prisma con un hueco cilíndrico y otro tórico de sección rectangular.




















una esfera a la que se le han restado dos pirámides de base cuadrada, una invertida respecto a la otra.























una esfera a la que se le ha quitado otra esfera, un prisma y un cilindro.

























esfera a la que se le ha quitado un octavo de la misma y varios cilindros y prismas.






























esfera en la que se ha practicado un hueco con forma de prisma de base pentagonal. La intersección de las caras del prisma con la esfera son circunferencias.























esfera en la que se ha practicado un hueco en forma de cilindro elíptico.



























esfera en la que se han practicado huecos con forma cilíndrica, esférica y tórica.























intersección de un prisma de base triangular y una esfera en la que se han practicado dos huecos, uno esférico y otro prismático.































pieza formada por una esfera a la que se le ha quitado un cuarto y en la que se ha practicado un hueco cilíndrico, otro cónico y otro tórico.




























esfera a la que se le ha quitado varios trozos de la misma, así como varios prismas y cilindros.


























esfera a la que se ha a restado un cubo interior, de manera que la zona de los vértices del cubo la atraviesan, dejando ver los ocho huecos correspondientes a la misma.




























esfera a la que se han quitado cilindros y un prisma.



























manera de mostrar el sistema diédrico la sección en el alzado de un detalle, y los detalles correspondientes a dos partes de la pieza A C. Las partes que se quieren resaltar se marcan con un círculo, se nombran y se dibujan a mayor escala en otra zona del papel indicando con una letra y entre paréntesis la escala que parte del dibujo se refieren.























Vistas diédricas de una pieza con su representación en axonometría y con el corte por el plano AA. En el corte sólo aparece representado lo que se ve detrás del plano de la sección tras girarlo 90° y proyectarlo en la dirección ortogonal al plano.


























figura cuyas tres proyecciones en planta, alzado y perfil tienen forma de H.



























prisma pentagonal en el que se han practicado dos huecos cilíndricos.


























En la pieza se ha hecho un corte con giro que pasa por los planos AA. Como estos planos son quebrados y la dirección del corte viene definida por la vertical (según vemos por la proyección ortogonal a este), a partir del punto donde se quiebra la línea por donde pasa el plano de corte -esto es, desde este punto hasta el final de la pieza, o sea, toda la zona horizontal- lo que aparece seccionado se gira hasta hacerlo coincidir con el plano vertical.



















aquí observamos un cono en planta, alzado y perfil. En él se han practicado tres huecos materializados en tres nuevos conos.


























en un prisma se han realizado dos huecos cilíndricos en una dirección y otro en otro.
El resultado de ambas interferencias en planta es una figura con una forma aproximada entre circunferencia y cuadrado.
























en un cubo se han practicado dos huecos cilíndricos tangentes en sus bases.



























esta figura es el resultado de la interferencia entre un prisma pentagonal y un prisma triangular.


























en un prisma se han practicado sobre sus aristas verticales cuatro huecos en forma de cono y por su eje un hueco cilíndrico.

























una figura semejante a la anterior pero sin el hueco cilíndrico interno.























una figura formada por la intersección de dos cilindros dejando un hueco en el interior con forma de cilindro y prisma y con un nexo de unión entre los trozos que quedan.


























En un prisma se ha practicado un hueco cónico que deja ver en su intersección vertical dos curvas hiperbólicas y en la horizontal una circunferencia.





























a un cono se le han practicado hueco cónico y otro cilíndrico.





























En un octaedro regular (dipirámide), que es un poliedro formado por dos pirámides unidas por sus bases y de caras triangulares equiláteras, se le ha restado una esfera interior cuyo centro coincide con el de la figura. Como todas las caras tienen la misma disposición respecto al centro tenemos que todas las secciones o huecos que produce la esfera son iguales. Observamos que la proyección auxiliar en los tres ejes o distancia entre vértices son iguales, el que corresponde a los vértices que se observan en la planta y el que corresponde a los vértices que comprende la línea vertical.






















aquí tenemos otro octaedro regular con diferentes proyecciones al que se le ha restado un cilindro.
































en un cubo se han practicado dos huecos, unos cilíndrico y otro prismático de sección pentagonal regular. En el alzado una sección meridiana proyecta las curvas elípticas de la interferencia de las dos superficies.


























en un cubo se han practicado dos huecos en forma de prisma de base triangular por dos de sus caras.






























pieza compuesta de prisma y cilindro con un hueco cilíndrico y otro prismático.

























en una esfera se hace un cono de base tangente por uno de sus diámetros dividiendo a la misma en dos partes, la que aparece en verde y la amarilla. El hueco cónico perfora a la semiesfera amarilla dejando ver el interior del mismo en color rojo.


























un prisma de base hexagonal es ahuecado por un cilindro ubicado en su interior de forma oblicua. En el dibujo tenemos proyecciones distintas y vistas auxiliares de la figura.























la figura está formada por la intersección de un cilindro y un prisma de base triangular. Por el eje de la figura se ha practicado otro hueco con forma de cono.


























La figura es una esfera a la que se le han restado tres piezas: un prisma interno, un cilindro interno que es tangente a las caras del prisma y un prisma que atraviesa la esfera quitándole un cuarto de la misma.






















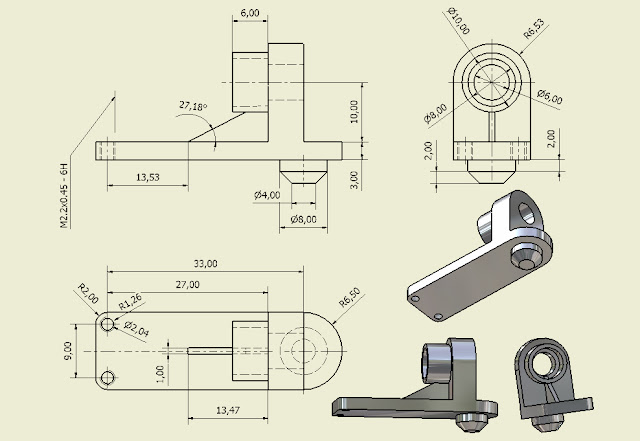
En la pieza observamos la acotación siguiendo la norma UNE. Como principios básicos de la acotación tenemos que por ser la pieza simétrica se determinan primero los ejes de simetría que aparecen definidos por segmentos alternos cortos y largos.
Una vez que hemos colocado los ejes marcamos la distancia entre los mismos. A continuación ponemos la cota de las circunferencias y de los arcos de la figura. Si no se marca el centro aparece el símbolo de diámetro, si el arco es mayor de 180° se acota como diámetro si es menor o igual se hace como radio. Para acotar el radio se pone la letra R si la línea de cota no pasa por el centro.



















En la figura observamos un prisma al que se le practicaron dos huecos cilíndricos, uno de ellos enlazado con un trozo de esfera tangente. La intersección de ambos cilindros viene determinada por las generatrices comunes y por la curva alabeada intersección de la esfera y cilindro que enlaza ambas. La curva alabeada se determina por la curva de intersección del plano que corta a la esfera y el que corta al cilindro. Cada plano determina un punto de la curva alabeada.






















En la figura observamos un toro sin agujero, esto es, la figura engendrada por una circunferencia que gira en torno a una secante no incidente en su centro. En el interior del toro se ha practicado un hueco prismático hasta la mitad de la figura, a partir de la mitad de la figura se toma la mitad del rombo que es la base del prisma y se gira en torno a uno de los ejes del rombo generando una superficie de revolución hueca en el interior de la figura y que pasa por la base del prisma hacia abajo.






















Cubo al que se restado un prisma hueco en su interior.





















Cilindro en el que se ha practicado un hueco cilíndrico en su interior. Como podemos observar los cilindros son tangentes en sus generatrices, ello provoca en el perfil un hueco en forma de pajarita.


























Un cubo es atravesado por dos cilindros huecos y por un prisma sólido oblicuo sólido dentro de él.























Aquí observamos en amarillo una llave con sus tres proyecciones diédricas, planta, alzado y perfil. A su derecha tenemos una proyección oblicua de la llave en planta con sus proyecciones correspondientes correlativas.
Una proyección cualquiera de estas últimas podría ser una representación axonométrica, ya que ésta es una proyección cilíndrica ortogonal sobre el plano, al igual que lo es el sistema diédrico. Por ello una de las cuestiones importantes en diédrico es que debemos utilizar para las proyecciones de la pieza vistas que sean representativas de sus dimensiones y que muestren sus caras en verdadera forma en la mayor medida de lo posible.















En la figura podemos observar las vistas diédricas de una pieza. A la derecha de la misma tenemos tres proyecciones axonométricas de la misma. En los planos de objetos y piezas industriales interesa utilizar una perspectiva para que se visualice mejor la pieza. Esta perspectiva conviene que sea una axonométrica ya que es una perspectiva en la que las paralelas se mantienen, esto quiere decir que si la pieza tiene aristas paralelas en el dibujo axonométrico persisten.













en la figura podemos observar una esfera en la que se han practicado dos huecos, uno formado por un cilindro vertical y otro formado por la composición de dos conos con la misma base.























en la figura podemos observar una esfera a la que se han restado tres cilindros ortogonales.





















Figura formada por prismas enlazados con arcos que generan en su extrusión superficies de revolución de sección rectangular.
























En la figura observamos la unión de seis conos con un prisma de base hexagonal.
Las superficies de los conos son tangentes a las caras verticales del prisma por la parte superior mientras que por la parte inferior cortan a la base del prisma según hipérbolas.
Los conos interiores tangentes en sus generatrices están representados en color azul por la parte superior y en color verde por la parte inferior mientras que los exteriores aparecen de color amarillo por la parte superior y en color naranja por la inferior.



















prisma con huecos generados por la intersección de tres cilindros.






















en una esfera se han practicado seis huecos esféricos que se interceptan entre sí.

























en la esfera se han practicado los seis huecos de la figura anterior, se han practicado otros seis huecos simétricos respecto a un plano meridiano de la esfera y en el interior de la misma se ha practicado otro hueco esférico que al mismo tiempo intercepta a las 12 esferas.



























En la figura observamos un cilindro que es atravesado por otro cilindro, generando como intersección de las dos superficies dos elipses y cuatro piezas idénticas.
La vista auxiliar proyectada en la dirección A transforma una de las elipses en una recta y la otra la mantiene invariable, por ser coincidente la elipse con el plano de proyección.




















Figura formada por un cubo al que se le ha practicado un hueco en forma de cubo.
Dentro del hueco contiene una media esfera centrada.





















La figura está formada por la unión de un prisma y un cilindro en la que se ha practicado un hueco prismático.
























figura formada por un cilindro atravesado por dos cilindros ortogonales horizontales, por un prisma cuyo eje pasa por el de la figura y por un cono en la base del cilindro en el que se practica un hueco con forma de pirámide.





















en una figura formada por un prisma y un cilindro se practican tres huecos generados por distintos conos.


























una figura contiene dos toros interiores que empiezan siendo huecos por su exterior y luego se convierten en sólidos.



























un prisma es atravesado por varios cilindros provocando esta forma irregular.

























aquí tenemos otro prisma atravesado también por varios cilindros en direcciones ortogonales.























una pieza muestra sus vistas diédricas y un alzado con una sección a un cuarto imaginaria.



























en la figura se observa un objeto formado por la intersección de un cono y un prisma. La intersección de las caras del prisma con la superficie cónica provoca dos hipérbolas, curvas que determinan al unirlas una superficie llamada cilindro hiperbólico. Al cono se le ha restado el cilindro hiperbólico sólido anterior provocando la figura que se observa en la representación.

























en la figura observamos un cono al que se le ha restado un cilindro en cuyo extremo se apoya una semiesfera. Como el cilindro es tangente a la base una generatriz es coincidente con él, por lo que aparece de forma continua. La esfera es tangente al cono por lo que la circunferencia de intersección o contacto entre ellas separa al cono en dos partes, la azul y la amarilla.






















en el prisma se han practicado tres huecos cilíndricos, dos concéntricos que pasan por los vértices y otro que pasa por los puntos medios de dos aristas opuestas.























prisma al que se le han restado varios cilindros.




























una esfera contiene en su interior dos pirámides huecas unidas por sus bases. En cada uno de los lados o caras de las pirámides se han levantado prismas huecos hasta el exterior. La figura es por tanto una esfera con seis prismas huecos de sección triangular dirigidos hacia el centro de la misma.

























en una esfera se han practicado tres huecos, uno prismático y otros dos cilíndricos concéntricos.
























un cono al que se le ha restado una pirámide de base hexagonal regular.





























la figura está generada por la intersección de dos prismas ortogonales de base triangular, uno en la dirección de planta y otro en la dirección del alzado, de ahí que sus dos proyecciones en planta y alzado sean triángulos equiláteros. A continuación se le ha practicado un hueco cilíndrico en la dirección vertical, lo que provoca que se vea en el perfil una curva elíptica.

























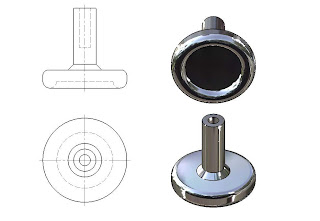
En la figura observamos una pieza compuesta por un cilindro hueco, roscado en su interior y una esfera unida al cilindro. La representación en alzado muestra un corte imaginario de la pieza como si se le hubiera quitado un cuarto.

























la figura está compuesta por tres piezas: una esfera de color amarilla en el centro con un hueco cilíndrico interior cuyo eje pasa por el centro de la misma y en cuyas bases del cilindro aparecen apoyados dos casquetes esféricos de color rojo y azul respectivamente.























la figura está compuesta por la intersección de dos cilindros sólidos y otra intersección interna de dos cilindros huecos.



























La pieza está formada por un cilindro al que se le ha restado en su interior cuatro trozos de esferas que suman entre sí 180°. La intersección con los trozos de esferas produce en las bases del cilindro sectores circulares cuyo ángulo es de 45° y en la superficie cilíndrica rectángulos adecuados a la misma. Las paredes internas planas aparecen de color azul mientras que las esféricas de color naranja.























la figura está formada por un toro (figura en forma de donuts) al que se le ha restado un cilindro tangente a la superficie y a la circunferencia del perfil en su base.

























la figura está formada por la intersección de un cilindro con seis toros que están dispuestos en una matriz polar. La intersección del cilindro y los toros provoca las "circunferencias" deformadas alabeadas azules mientras que las superficies de los toros aparecen en color amarillo.

























la figura muestra una esfera a la que se le ha restado un prisma interior. El prisma corta a la esfera según planos que son circunferencias. En la proyección en planta observamos que la base del prisma es un cuadrado. Si todas las proyecciones fueron cuadradas las circunferencias estarían unidas entre sí por un único punto, con lo cual la figura se descompondría en tantos casquetes esféricos como lados tiene el cubo. Como observamos en la vista auxiliar, la altura distinta de la base provoca que no sea un cuadrado perfecto, con lo que la superficie esférica enlaza los casquetes por una región mayor que por un punto, de ahí que sea una sola pieza y no varias.
















una elipse en la revolución de su eje menor provoca un elipsoide. En él se practican varios huecos, uno cilíndrico y los otros cónicos y cilíndricos correspondientes al interior amarillo.












Hay piezas especialmente complicadas de resolver, como por ejemplo la de este dibujo.
Tal y como aparece en el dibujo parece sencilla, pero si proponemos a un alumno que la resuelva dándole sólo como datos la planta y alzado de la figura, tendrá gran dificultad para obtener la perspectiva axonométrica de la figura


Figura formada por un prisma al que se le han enlazado aristas adyacentes, además de ser agujereado por un par de cilindros y un prisma.

Esfera en la que se han practicado varios huecos cónicos interiores y al mismo tiempo se le ha restado parte del sólido.




Figura




es
Esfera con 2 prisma huecos
Figura formada por un cilindro en el que se han practicado un par de huecos cilíndricos.












































































































Teorema de Monge


Si a 3 circunferencias se le hacen las tangentes comunes 2 a 2, los 3 puntos de intersección de cada par de tangentes están alineados. El teorema es válido para las tengentes exteriores e interiores, indistintamente y combinadas.





Una aplicación la tenemos en el siguiente ejercicio generalizado el teorema anterior en el espacio.
Dadas 3 esferas determinar las trazas del plano que se apoya en ellas.
Hacemos los 3 conos tangentes a ambas -como cucuruchos que contienen bolas de helado-, y en los 3 vértices de los conos está la traza del plano. Hacemos una posible proyección en alzado con la LT perpendicular a la traza horizontal para facilitar el ejercicio y la traza vertical la pasamos tangente a los alzados de las esferas. En los puntos de tangencia se apoya el plano, detalle que se puede bajar a la planta.

http://teoremas-de-geometria.blogspot.com/2012/03/teorema-de-monge.html













Desarrollo de una superficie.
http://desarrollo-de-superficies.blogspot.com.es/

El desarrollo de una superficie es la figura plana obtenida al extenderla sobre un plano. Es como si una figura estuviera envuelta por un material fino en su superficie que se abriera a lo largo de las aristas. Al ir abriendo cada una de sus caras las doblaríamos hasta situarlas en un plano del dibujo, quedando extendido el envoltorio de la figura sobre el plano.
Al desarrollar la figura sobre un plano se obtiene el verdadero tamaño y forma de las caras.



Para construir el desarrollo de una pirámide, hacemos un giro de sus caras tomando como eje de giro la arista del plano t2 correspondiente a la base. Para hacer el giro proyectamos el vértice de la pirámide O sobre el plano horizontal y desde este punto O’ hacemos una recta perpendicular m2 a la traza del plano t2 correspondiente a la cara. Haciendo centro en el punto Z2 de intersección de esta perpendicular con la traza del plano, hacemos un giro tomando como radio la distancia desde el centro Z2 hasta el vértice de la pirámide O. El arco correspondiente al giro de vértice O determina en la intersección con la perpendicular m2 a t2 el vértice abatido (O2), que unido a los extremos de la traza de la cara t2 constituye la cara abatida de la pirámide (en el dibujo aparece en color rojo).
Las tres caras abatidas junto con la base de la figura determinan la figura extendida sobre el plano, en geometría se llama el desarrollo de la misma. Podemos doblar los triángulos rojos por los lados que tocan a la base de la figura (t1 t2 t3) y se construye así la pirámide en tres dimensiones.

En el dibujo vemos el ejercicio resuelto en el sistema diédrico. Para hacer el abatimiento de las caras, tomamos una de ellas, por ejemplo aquella cara cuyo plano corta al horizontal según la recta t2. Haciendo desde el vértice de la pirámide una perpendicular a esta recta m2 y tomando el punto de intersección de ambas Z2, hacemos centro en él con la distancia desde ese punto Z2 hasta el vértice de la pirámide abatida O2’. Para hacer el abatimiento de ese triángulo que está en un plano vertical tomamos la altura del vértice de la pirámide h que está en el alzado en verdadera magnitud y la colocamos a partir del vértice en planta O ortogonalmente a la recta m2. De esta manera obtenemos el vértice de la pirámide abatido O2’ y la pendiente de la cara, definida por los puntos Z2-O’2.
A continuación haciendo centro como habíamos dicho en la intersección de la perpendicular a la traza de la cara, en Z2, hacemos el arco con el radio Z2-O’2 y donde corte este arco a la prolongación de la perpendicular m2 tenemos el vértice de la pirámide abatida (O2) y por tanto el abatimiento de esta cara, ya que los otros: al estar en el eje del giro, permanecen inalterables. Este punto se une con los extremos de t2 y tenemos toda la cara abatida.
Para abatir las otras dos caras procedemos de igual forma. Las tres caras triangulares abatidas (en color rojo) junto con la base de la figura (en color amarillo) definen el desarrollo de la pirámide oblicua, con lo que se podría recortar el contorno y doblar por la intersección de cada triángulo rojo con el amarillo, obteniendo de esta manera la figura construida, por ejemplo en papel.



Un ejemplo de un poliedro de Catalan -en color magenta- y su desarrollo, inscrito además en su dual, el cubo truncado.

Octaedro triakis y su dual, como el primero tiene 24 caras, 14 vértices y 38 aristas, el segundo (Cubo Truncado), que es su dual, tiene el mismo número de aristas (38), 24 vértices y 14 caras.
http://desarrollo-de-superficies.blogspot.com.es/
http://poliedrosdecatalanendiedrico.blogspot.com.es/



Tipos de desarrollos:

Se puede desarrollar mediante líneas que pasan por un centro, también llamadas radiadas.
Una figura se puede desarrollar mediante líneas paralelas como pasa con las superficies radiadas de vértice impropio: los prismas y cilindros. Este desarrollo corresponde a superficies radiadas de punto impropio como son las pirámides y los conos.

Mediante triangulaciones, esto se obtiene al dividir las caras de la superficie en formas triangulares.

Desarrollos aproximados, son los que se utilizan para las superficies alabeadas y de doble curvatura, superficies que no se pueden desarrollar pero que se pueden obtener formas aproximadas de su extensión sobre el plano.



Páginas de figuras en sistema diédrico:

http://piezas-vistas-y-cortes-1.blogspot.com/
http://piezas-vistas-y-cortes-2.blogspot.com/
http://piezas-vistas-y-cortes-3.blogspot.com/
http://piezas-vistas-y-cortes-4.blogspot.com/
http://piezas-vistas-y-cortes-5.blogspot.com/
http://piezas-vistas-y-cortes-6.blogspot.com/
http://piezas-vistas-y-cortes-7.blogspot.com/
http://piezas-vistas-y-cortes-8.blogspot.com/
http://piezas-vistas-y-cortes-9.blogspot.com/
http://piezas-vistas-y-cortes-10.blogspot.com/
http://piezas-vistas-y-cortes-11.blogspot.com/
http://piezas-vistas-y-cortes-12.blogspot.com/
http://piezas-vistas-y-cortes-13.blogspot.com/
http://piezas-vistas-y-cortes-14.blogspot.com/
http://piezas-vistas-y-cortes-15-poliedros.blogspot.com/
http://piezas-vistas-y-cortes-16.blogspot.com/
http://piezas-vistas-y-cortes-17.blogspot.com/
http://piezas-vistas-y-cortes-18.blogspot.com/
http://piezas-vistas-y-cortes-19.blogspot.com/
http://piezas-vistas-y-cortes-20.blogspot.com/
http://piezas-vistas-y-cortes-21.blogspot.com/
http://dibujo-de-piezas.blogspot.com/
Publicado por en 3 comentarios:
Suscribirse a: Entradas (Atom)