El sistema diédrico: Ángulos

Para calcular el ángulo que forman dos rectas en sistema diédrico se abaten hasta hacerlas coincidir con plano de proyección. El ángulo se define como el menor de los 2 ángulos que forman.

Para calcular el ángulo que forman dos planos se hace un plano perpendicular a ambos (o sea, a su recta de intersección), éste los corta según dos rectas y el ángulo que forman éstas es la solución. A partir de aquí el ejercicio es como el anterior.

Para calcular el ángulo que forman una recta y un plano se toma un punto de la recta y desde la misma se hace una perpendicular al plano. En la intersección de la nueva recta y el plano tenemos un punto que unido al de intersección de la recta dada y el plano obtenemos otra recta. El ángulo que forma esta recta y la dada es la solución.

En el dibujo dos rectas a b se cortan según un ángulo alfa. Se unen las trazas de las rectas a b mediante una recta que es la traza del plano que se va a abatir. El punto de intersección P de las dos rectas al ser abatido caerá en la perpendicular a la traza del plano. El centro del giro para hacer el abatimiento está en el punto O, punto de intersección de la perpendicular que pasa por P y por la traza del plano que contiene a las rectas a b. Al hacer centro en el punto O tomando como radio la distancia OP, hacemos un arco que corta en el plano de la planta en el punto (P). Este punto Abatido lo unimos con las trazas de las rectas a b y nos determina las rectas abatidas (a) (b). Como ese giro no se puede hacer en el espacio en el sistema diédrico, lo hacemos sobre el plano de la planta, para ello hacemos desde el punto que una perpendicular al plano de la planta del dibujo y obtenemos el punto P1. La distancia P-P1 colocamos en la planta a partir del punto P1 y perpendicular a la proyección en planta de la recta OP. Tenemos por tanto que la distancia P-P1 sobre la planta se transforma en la distancia (Pa)-P1. Haciendo centro en el punto O con la distancia O (Pa) hacemos un marco hasta que corta a la línea O-P1 en el punto (P). Unimos este punto con las trazas de las rectas y tenemos las rectas abatidas cuyo ángulo menor es el que forman a b.

Dos rectas oblicuas en sistema diédrico s r, hacemos una línea horizontal en el plano vertical que corta a las mismas según los puntos 1’ 2’, y éste es el nuevo plano horizontal considerado para hacer el abatimiento arriba mencionado.
A partir de aquí se hace un giro del punto de intersección de las dos rectas y obtenemos su abatimiento (A). Uniendo este punto con los puntos 1 2 tenemos las dos rectas abatidas con el ángulo que forman, que es el menor de los dos.

Se trata de calcular el ángulo que forman las rectas b m. Se coge un punto cualquiera de la recta b, por ejemplo el punto P, y se hace una recta paralela a la dada m, por el punto P.
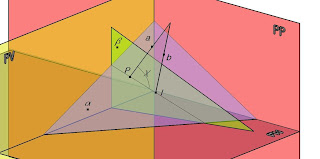
Las dos rectas a b determinan un plano cuya traza horizontal es la recta azul y va a ser el eje del giro del triángulo de lados a b h cuyo ángulo entre las dos rectas aparece en amarillo en planta y alzado.
Al abatir el triángulo tenemos el nuevo triángulo con el ángulo verde que forman las dos rectas en verdadera magnitud.

Ángulo que forma una recta b y un plano alfa. Desde un punto cualquiera de la recta b se hace una perpendicular al plano alfa y corta a éste en el punto P, que unido con el punto I de intersección de la recta b y el plano alfa, tenemos dos rectas: la recta PI y la recta b, el ángulo que forman estas dos rectas es el ángulo que forma el plano alfa y la recta b.

Otro ejemplo como el anterior, una recta a y un plano f, se trata de determinar el ángulo entre ambas. Por un punto cualquiera P de la recta a se hace una perpendicular al plano hasta que lo corta en el punto T. Se une este punto con la intersección de la recta y el plano que es el punto M. El ángulo que forman las rectas: a T-M, es el ángulo que forma la recta y el plano.

Calcular el ángulo que forma la recta a y el plano alfa del sistema diédrico.
Se coge un punto cualquiera de la recta a, por ejemplo el punto P y se hace una recta r perpendicular al plano (la que tiene las proyecciones perpendiculares a las trazas del plano). La recta r corta al plano según el punto M (para calcular la intersección de una recta y un plano se pasa un plano por la recta, se calcula la recta de intersección de los dos planos y su intersección con la recta dada es el punto de intersección de la recta con el plano), que unido a la intersección I de la recta a y el plano alfa, tenemos la recta IM.
El ángulo que forman las rectas MI a, es el ángulo que forma la recta y el plano dados. Partir de aquí el ejercicio se reduce al ángulo entre dos rectas.

Para calcular el ángulo que forman dos planos (en el dibujo de colores azul y rojo) se hace un plano perpendicular a la intersección de los mismos. Este plano corta a los planos dados según dos rectas a b, el ángulo n de estas dos rectas es el ángulo que forman los planos.

Para calcular el ángulo que forman dos planos (en el dibujo de colores azul y rojo) se hace un plano perpendicular a la intersección i de los mismos, este plano por ser perpendicular a la recta i de intersección tiene su traza t perpendicular a la proyección de la recta. Este plano corta a los planos dados según dos rectas a b, para saber el ángulo que forman estas dos rectas, tendremos que abatir las respecto a la traza t del plano que las contiene. El ángulo que forman las dos rectas es el ángulo que forman los planos.

Aquí tenemos el ejercicio anterior resuelto el sistema diédrico. Tenemos que la traza del plano X1 es perpendicular a la recta de intersección a, por tanto al abatir la recta (a) tendremos que hacer una perpendicular a ella desde el punto de intersección de a1 con la traza del plano x1, obteniendo de esta forma el punto P1 que proyectado sobre la recta a1 se transforma en el punto P1’. Si unimos este punto con las trazas de las rectas tenemos dos rectas cuyo ángulo entre ellas es el ángulo entre los dos planos.

Dados los ángulos que forma una recta con los planos de proyección en sistema diédrico, determinar las proyecciones de la recta.

Tenemos por ejemplo los ángulos dados: 30,96° y 37, 51°.

Hacemos una proyección horizontal de la recta cualquiera, por ejemplo CB. Colocamos el ángulo 30,96° en uno de los extremos del segmento, por ejemplo por el punto C. Por el punto opuesto B hacemos una perpendicular h hasta que corte a la línea que hicimos por C bajo un ángulo de 30,96°. En la intersección de esa línea CD y la perpendicular h tenemos el punto E. de esta forma tenemos el triángulo amarillo que es el abatimiento del segmento CB en planta y que determina ya la medida real de la recta, que es CE. Esa medida saldría de distinto tamaño si la dimensión de CB la variamos, pero es un dato irrelevante en el ejercicio, en el que realmente se piden unos ángulos, sin importar las dimensiones de la recta.

Hacemos centro en el punto C con la distancia CE y construimos una circunferencia, a continuación tomamos un radio cualquiera de esta circunferencia, por ejemplo CG. A partir del punto G tomamos el ángulo dado, 37,51°, y en la intersección con la perpendicular u desde C a esta nueva recta w obtenemos el punto J.

Tomamos centro en C y con la distancia radial CJ hacemos una circunferencia hasta que corte a la semi circunferencia de diámetro CB en el punto K. La recta KB es la línea de tierra, por lo que ya podemos construir la proyección vertical de la recta, vendrá dada por KI, sabiendo que el punto I es la intersección de la perpendicular m a la línea de tierra KB con el arco de color verde de centro B y radio BE.

La recta KI es la proyección vertical de la recta que forma 37, 51° con el plano vertical, y lo podemos comprobar si hacemos centro en el punto K con la distancia KC hasta que corta a la perpendicular r al segmento KI. Como podemos comprobar el triángulo rosa ILK tiene en el vértice I el mismo ángulo 37,51°, ya que es el abatimiento de la recta sobre el plano vertical y nos muestra el ángulo que forma la misma con ese plano.

-----------------------------------------------------------------------------------------

Trazar un plano que forme 55 grados con el plano horizontal y 46 grados con el plano vertical.

El cono verde de Vértice P es aquel que cumple la condición de que todos los

planos tangentes a él forman 55 grados con el plano horizontal

El cono azul de Vértice V cumple la condición de que todos los planos

tangentes a él forman 46 grados con el plano vertical

Como ambos conos están circunscritos a una esfera e, necesariamente ésta

es tangente al plano que forma ambos ángulos dados con el plano horizontal y vertical,

en consecuencia la traza vertical a2 del plano pasará por el punto P y será tangente
a la circunferencia s del cono azul mientras que la traza horizontal a1 pasará por el vértice V

y será tangente a la circunferencia t del cono verde.

Como las trazas de un plano se cortan en la línea de tierra, a1 y a2 se cortarán en

un mismo punto sobre la misma.

-----------------------------------------------------------------------------------------

Otros 2 ejemplos de rectas dados los ángulos: