Una recta pertenece a un plano o incide en él si sus trazas están sobre las trazas del plano.
Un punto pertenece a un plano si está sobre una recta del plano.
Un punto pertenece a una recta si las proyecciones del mismo están sobre las proyecciones de la recta.
En los tres casos la recíproca es cierta, pudiendo eliminar las excepciones si utilizamos los 3 planos de proyección (planta, alzado y perfil).
-----------------------------------------------------
La recta a pertenece al plano por tener sus trazas sobre las trazas del plano.

En diédrico: la recta r tiene sus trazas sobre las trazas del plano y al mismo tiempo es una recta de máxima pendiente del plano alfa por tener su proyección horizontal perpendicular a la traza horizontal del plano.
La recta de máxima pendiente es la que describiría un objeto que cayera por el plano, siguiendo la distancia más corta.

-----------------------------------------------------
Tenemos otra recta incidente en el plano pero de máxima inclinación por tener su proyección vertical perpendicular a la traza vertical del plano. Como la perpendicular a la traza vertical es la distancia más corta a la recta, en la práctica una recta de máxima inclinación sería la trayectoria de un móvil que se desplaza por el tejado (por el plano oblicuo) y que buscara al mismo tiempo la distancia más corta hacia el plano vertical.

Si dos rectas se cortan determinan un plano, por lo que las trazas verticales de ambas pertenecen a la traza vertical del plano y las horizontales a la horizontal del plano.
Como las rectas se cortan en un punto común y las proyecciones de un punto siempre quedan en una vertical, las rectas se cortan en un punto cuyas proyecciones P1 P2 están alineadas en la vertical.

-----------------------------------------------------
Como las trazas de una recta que pertenece a un plano están en las trazas de éste, tenemos que la traza horizontal de la recta frontal Hr está sobre la traza horizontal del plano y la traza vertical de recta y plano inciden ya que por ser paralelas se cortan en el mismo punto, el del infinito.

-----------------------------------------------------
Si consideramos ahora el plano de planta como en el alzado y éste como el de planta, la recta anterior se transforma en horizontal. La recta horizontal r pertenece al plano y el punto A a la recta r por tener su proyecciones sobre las de la recta. El punto pertenece también al plano por estar contenido en una recta del mismo.

-----------------------------------------------------
Si una recta y plano inciden y la recta tiene su proyección horizontal paralela a la traza horizontal del plano, la proyección vertical de la recta es horizontal ya que si el plano es cortado por el plano horizontal de proyección según una dirección, un plano que seccionara al horizontal por la recta r provocaría las mismas direcciones en las secciones que el anterior: en planta una paralela a la traza y en alzado una paralela a la línea de tierra (según el teorema de que planos paralelos producen secciones paralelas).

-----------------------------------------------------
Un punto P perteneciente a un plano que pasa por la línea de tierra. Las proyecciones en planta y alzado del punto no serían suficientes para determinar si pertenece al plano, para ello se hace necesario dibujar el perfil del plano e incidir P’’’ sobre el mismo.

-----------------------------------------------------
Los próximos 4 ejercicios son rectas oblicuas incidentes en los siguientes planos: de canto o proyectante vertical, paralelo a la línea de tierra, oblicuo y vertical.




Los ejercicios anteriores resueltos en sistema diédrico con las trazas de las rectas en las trazas de los planos respectivos.

-----------------------------------------------------
Aquí tenemos distintos planos con rectas incidentes en los mismos:
o- oblicua, h- horizontal, p- de perfil, t- que pasa por la línea de tierra, f- frontal, a- paralela a la línea de tierra, u- de punta, v- vertical.

Aquí podemos observar el mismo dibujo en sus proyecciones diédricas en planta y alzado.

-----------------------------------------------------
 Dados dos puntos B A que están situados en el segundo y cuarto cuadrante respectivamente, determinar las proyecciones de la recta que pasa por los dos puntos. Los puntos tienen por proyecciones B1 B2 A1 A2, se unen las proyecciones del punto del plano horizontal entre sí A1 B1 y de igual forma las del plano vertical A2 B2 así obtenemos las dos proyecciones de la recta, que son m1 m2.
Dados dos puntos B A que están situados en el segundo y cuarto cuadrante respectivamente, determinar las proyecciones de la recta que pasa por los dos puntos. Los puntos tienen por proyecciones B1 B2 A1 A2, se unen las proyecciones del punto del plano horizontal entre sí A1 B1 y de igual forma las del plano vertical A2 B2 así obtenemos las dos proyecciones de la recta, que son m1 m2.Donde la proyección horizontal m1 corta a la línea de tierra, levantamos una vertical y obtenemos la traza vertical de la recta Vm.
Donde la proyección vertical corta a la línea de tierra, hacemos una recta de punta por ese punto hasta que corte a la proyección horizontal de la recta, obteniendo así la traza horizontal de la misma, que es Hm.
Tenemos que la recta m es una recta oblicua que pasa por los puntos dados que están en otro cuadrante distinto y cuyo tramo visible en el primer cuadrante es el que está comprendido entre sus trazas.
 Aquí observamos el ejercicio en sistema diédrico, hemos unido las proyecciones horizontales entre sí A1 B1 y donde corta a la línea de tierra hacemos una vertical. En la intersección de esta vertical con el segmento que une los dos puntos correspondientes a la proyección vertical A2 B2, tenemos la traza vertical de la recta, Vm.
Aquí observamos el ejercicio en sistema diédrico, hemos unido las proyecciones horizontales entre sí A1 B1 y donde corta a la línea de tierra hacemos una vertical. En la intersección de esta vertical con el segmento que une los dos puntos correspondientes a la proyección vertical A2 B2, tenemos la traza vertical de la recta, Vm.De igual forma la proyección vertical de la recta m2 corta a la línea de tierra en un punto por el que bajamos una vertical y donde ésta corta a la proyección horizontal m1 tenemos la traza de la recta Hm.
-----------------------------------------------------
 En este caso tenemos la representación espacial de una recta oblicua definida por un punto del primer cuadrante A y otro del tercero B. Operamos de la misma forma que en el ejercicio anterior, unimos las proyecciones horizontales A1 B1 y donde corte a la línea de tierra hacemos una vertical, en la intersección de esta vertical con la proyección vertical de la recta obtenemos la traza vertical de la misma Vm.
En este caso tenemos la representación espacial de una recta oblicua definida por un punto del primer cuadrante A y otro del tercero B. Operamos de la misma forma que en el ejercicio anterior, unimos las proyecciones horizontales A1 B1 y donde corte a la línea de tierra hacemos una vertical, en la intersección de esta vertical con la proyección vertical de la recta obtenemos la traza vertical de la misma Vm.Análogamente unimos las proyecciones verticales de los puntos y donde corta el segmento de unión de ambos a la línea de tierra hacemos una recta perpendicular a la misma y que esté en el plano horizontal. Esta recta corta a la proyección horizontal en la traza horizontal de la recta Hm.

El ejercicio resuelto en sistema diédrico: los puntos dados de la proyección horizontal A1 B1 se unen hasta que cortan a la línea de tierra en un punto, por éste se hace una recta vertical hasta que corte a la recta que une los dos puntos A2 B2, que es la proyección vertical de la recta. En la intersección de la proyección vertical de la recta m2 con esta vertical obtenemos la traza vertical de la recta Vm.
De igual forma unimos A2 B2 de la proyección vertical y donde esta recta corte a la línea de tierra hacemos una recta vertical que corta a la proyección horizontal en un punto Hm que es la traza horizontal de la recta. Observamos en esta recta en el ejercicio resuelto en el espacio que sólo tiene su tramo continuo en el primer cuadrante en la porción comprendida entre la traza vertical Vm y el punto A.
-----------------------------------------------------
 Dados dos puntos que están situados en el segundo y cuarto cuadrante, se pide determinar las proyecciones de la recta que pasa por estos dos puntos.
Dados dos puntos que están situados en el segundo y cuarto cuadrante, se pide determinar las proyecciones de la recta que pasa por estos dos puntos.Procedemos como en los ejercicios anteriores, unimos las proyecciones de los puntos del plano horizontal A1 B1 hasta que corten a la línea de tierra en un punto por el que hacemos una vertical, donde esta corte a la proyección vertical de la recta tenemos la traza vertical de la recta Vm. Operamos de igual forma para obtener la traza horizontal de la recta Hm.
Como esta recta pasa por el segundo, tercero y cuarto cuadrante, tenemos que ninguna de sus dos proyecciones, horizontal y vertical, son percibidas o vistas directamente en el primer cuadrante, de ahí que sus dos proyecciones deben aparecer discontinuas.

El ejercicio de antes resuelto en el sistema diédrico, se han unido los dos puntos, por un lado las dos proyecciones horizontales de los dos puntos A1 B1y por otro lado las dos proyecciones verticales A2 B2 de los dos puntos. Al unir estas proyecciones tenemos las dos proyecciones de la recta m1 m2 que cortan a la línea de tierra en dos puntos por los que hacemos verticales. Éstas verticales por cada una de las proyecciones de la recta (m2), cortan a la otra proyección (m1) determinando las trazas de la recta Hm.
Para determinar las partes que son visibles de la recta es imprescindible su representación espacial, ya que si bien en el ejercicio resuelto es fácil seguir el proceso deductivo extrapolable por otros ejercicios también del sistema diédrico, la representación de la recta en el espacio nos determina qué parte está en cada cuadrante.
-----------------------------------------------------
 Dada una recta a (en el dibujo de color rojo) en el primer cuadrante definida por sus proyecciones y un punto exterior M situado en el segundo cuadrante, determinar el plano que pasa por ambos elementos.
Dada una recta a (en el dibujo de color rojo) en el primer cuadrante definida por sus proyecciones y un punto exterior M situado en el segundo cuadrante, determinar el plano que pasa por ambos elementos.Se une la traza vertical de la recta Va con el punto dado M y donde la prolongación de esta recta de unión corta al plano horizontal tenemos un punto R de la traza del plano, que unido con la traza horizontal de la recta Ha determina la traza horizontal del plano TR que contiene al punto y a la recta dados.
Donde la traza horizontal del plano corta a la línea de tierra -en el punto R-, tenemos que por este punto pasa la traza vertical del plano. Sólo hay que unir el punto R con la traza vertical de la recta Va y tenemos la traza vertical del plano Va-R.
El procedimiento se basa en que dos rectas determinan un plano cuando se cortan, por lo que se trazó una recta que cortara a la recta dada y al mismo tiempo pasara por el punto dado M.
 El ejercicio anterior resuelto en el sistema diédrico.
El ejercicio anterior resuelto en el sistema diédrico.Tenemos la recta a dada por sus proyecciones a1 a2 y el punto del segundo cuadrante M con sus dos proyecciones M1 M2, unimos la proyección vertical del punto M2 con la traza vertical de la recta Va y obtenemos en la prolongación de esta línea un punto de intersección con la línea de tierra por el que trazamos una vertical z.
Por la traza vertical de la recta Va hacemos una vertical hasta que corta en la línea de tierra en el punto P. Éste punto lo unimos con la proyección horizontal. del punto dado M1 hasta que corta a las recta vertical z en el punto T.
Unimos el punto T con la traza horizontal de la recta Ha teniendo un nuevo punto de intersección con la línea de tierra R. Unimos este punto R con la traza vertical de la recta Va y tenemos ya la traza vertical del plano Va-R.
-----------------------------------------------------
En este caso tenemos una recta que no pertenece al plano por no tener ninguna de sus trazas sobre las trazas del plano. Como sabemos para que una recta pertenezca al plano debe tener sus trazas sobre las trazas del plano o bien tener 2 puntos cualesquiera de ella sobre el plano, ya que una recta queda definida por dos puntos. Si la recta tiene 2 puntos cualesquiera sobre el plano quiere decir que todos sus puntos están sobre él y por tanto las trazas de la recta también estarán sobre las trazas del plano.
-----------------------------------------------------
En este dibujo tenemos un punto P perteneciente o un plano paralelo a la línea de tierra. Sabemos que pertenece a este plano porque pertenece a una recta del plano y como la recta tiene todos sus puntos sobre el plano el punto de la recta pertenece al plano.
Recta oblicua de máxima pendiente perteneciente al plano. Una recta a es de máxima pendiente cuando el ángulo que forma con la traza horizontal (alfa uno) del plano es de 90°. Si la recta es perpendicular a la traza del plano su proyección a1 también lo será.
-----------------------------------------------------
Recta de máxima inclinación de un plano. Una recta tiene máxima inclinación en un plano cuando la proyección vertical a2 de la misma es perpendicular a la traza del plano alfa dos. Aparte de tener su proyección perpendicular a la traza del plano tenemos que esta recta es perpendicular a la traza del plano vertical.
-----------------------------------------------------
En este ejercicio tenemos distintos casos de incidencia: en el número uno una recta vertical perteneciente a un plano vertical, en el número dos una recta oblicua perteneciente a un plano vertical, en el número tres una recta de perfil perteneciente a un plano paralelo a la línea de tierra, en el ejercicio número cuatro tenemos una recta oblicua perteneciente a un plano paralelo a la línea de tierra y en el número cinco tenemos un plano oblicuo que contiene una recta oblicua.
Para comprender un caso práctico de una línea de máxima pendiente y máxima inclinación sobre un plano podemos poner el siguiente ejemplo: considerando el plano oblicuo como un tejado, si tenemos por ejemplo una esfera en A y la dejamos caer por el tejado seguirá una trayectoria perpendicular a la línea de la base del tejado, es la trayectoria más corta siguiendo una línea de máxima pendiente.
Si tenemos sobre ese mismo tejado otro punto B donde por ejemplo se sitúa un operario al que se le pide que alcance el plano vertical correspondiente al muro de la casa que linda con el tejado, con la condición de que lo alcance siguiendo el camino más corto posible. El operario deberá seguir una trayectoria perpendicular a la intersección del tejado con el muro, esta línea perpendicular es en realidad la línea de máxima inclinación.
En este caso hemos dibujado distintos planos y rectas oblicuas que se pueden poner o incidir sobre ellos. Tenemos rectas oblicuas que pertenecen a los siguientes planos: una recta oblicua perteneciente a un plano paralelo a la línea de tierra en el caso número dos, en el número tres tenemos una recta oblicua que pasa por la línea de tierra sobre un plano que pasa por la línea de tierra, en el caso número cuatro tenemos una recta oblicua que pertenece un plano vertical, en el caso número cinco tenemos una recta oblicua que pasa también por la línea de tierra y es incidente en un plano primer bisector, que es aquel que biseca el primer cuadrante. En el caso número seis tenemos una recta oblicua sobre un plan oblicuo, en el caso número siete tenemos una recta oblicua sobre un plano proyectante vertical, en el número ocho tenemos una recta oblicua sobre un plano de perfil, que es aquel ortogonal a la línea de tierra.
-----------------------------------------------------
Una recta de punta es aquella que es perpendicular al plano vertical, sólo cabe sobre el plano número uno o plano horizontal, sobre el plano número siete o proyectante vertical o de canto y sobre el número ocho que es un plano de perfil.
-----------------------------------------------------
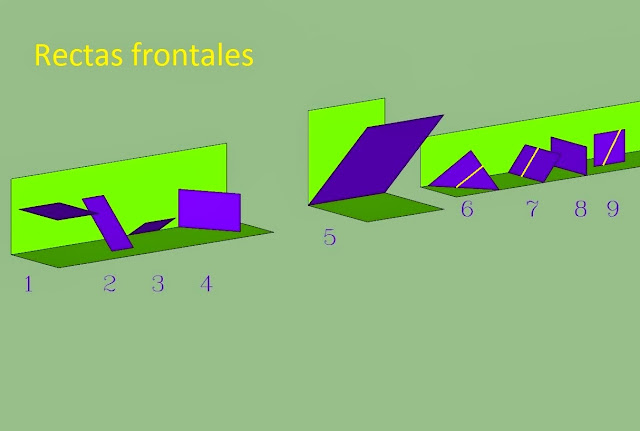
Una recta vertical se puede meter dentro de un plano vertical, como en el caso número cuatro o dentro de un plano de perfil, como en el caso número ocho o como en el 9 en uno frontal.
Una recta frontal es aquella que se puede colocar en un plano paralelo al plano vertical (caso número 6, 7 y 9) y es oblicua respecto al horizontal de proyección, como casos particulares tenemos la recta paralela a la línea de tierra y la línea vertical.
Las rectas horizontales pueden incidir sobre un plano horizontal en el caso número uno, en un plano paralelo a la línea de tierra en el caso número dos, sobre un plano que pasa por la línea de tierra en el 3, en este caso tenemos que la recta es paralela a la línea de tierra, aparte de ser horizontal, en el caso número cuatro la recta horizontal pasa por un plano vertical, en el caso número cinco es paralela a la línea de tierra y horizontal y pasa por el plano bisector, en el caso número seis la recta es horizontal y oblicua, en el caso número siete la recta es horizontal y perpendicular al plano vertical, por tanto es una recta de punta. En el caso número ocho tenemos que la recta es también de punta y al mismo tiempo una recta horizontal y en el caso número nueve tenemos una recta que se puede meter en un plano frontal siendo horizontal al mismo tiempo.
-----------------------------------------------------
Una recta de perfil es aquella que se puede meter en un plano de perfil, esto es, en un plano que es perpendicular a la línea de tierra. Tenemos como casos particulares de la recta de perfil aquella que pasa por la línea de tierra, aquella que es de punta y aquella que es vertical.
En el caso número uno tenemos la recta de perfil y de punta, sobre un plano horizontal, en el caso número dos tenemos una recta de perfil incidente en un plano paralelo a la línea de tierra. En el caso número tres tenemos una recta que pasa por la línea de tierra y por un plano incidente en la línea de tierra. En el caso número cinco tenemos otra línea que pasa por la línea de tierra siendo de perfil y pasando por un plano bisector. En el caso número seis tenemos una recta de perfil que incide en un plano oblicuo. En el caso número ocho tenemos una recta de perfil incidente en un plano de perfil.
-----------------------------------------------------
Una recta paralela a la línea de tierra es aquella que tiene sus puntos equidistantes con ésta, por tanto podemos colocar una paralela a la línea de tierra sobre un plano horizontal, como en el caso número uno, también lo podemos hacer sobre un plano paralelo a la línea de tierra, como en el caso número dos, también se puede poner una recta paralela a la línea de tierra sobre un plano que incide en la línea de tierra -3. Podemos colocar también la recta paralela a la línea de tierra sobre un plano bisector- 5, por ser un caso particular del número tres, por último en el caso número nueve hemos colocado una paralela a la línea de tierra en un plano frontal, que también tiene todas sus líneas paralelas a la línea de tierra ya que es un plano paralelo al vertical de proyección.
Las rectas que pasan por la línea de tierra son aquellas que tienen un punto sobre la misma, ya que si tuvieran los dos serían la misma línea de tierra. En consecuencia todos los planos que tengan un punto o más sobre la línea de tierra podrán contener a una recta que pase por la línea de tierra, como es el caso número tres. Un plano que pasa por la línea de tierra contiene a infinitas líneas que pasan por la línea de tierra. Parece que como un plano que pasa por la línea de tierra tiene esta línea sobre el mismo plano pues contiene infinitas rectas que pasan por los infinitos puntos de esta línea, pero eso sucede en todos los planos, aunque corten a la línea de tierra en un solo punto, ya que por un punto de un plano se pueden pasar infinitas rectas.
En el caso número cuatro un plano vertical contiene una recta o infinitas rectas que pasan por la línea de tierra, también tenemos un ejemplo concreto de una línea que pasa por la línea de tierra y pertenece al plano del bisector en el ejemplo número cinco, otro caso en el plano oblicuo en el número seis, otro ejemplo en el número siete con un plano proyectante vertical y por último en el caso numero 8 un plano de perfil contiene a una línea que pasa por la línea de tierra.
-----------------------------------------------------
Dadas las rectas características de un plano, determinar las trazas del mismo.
Las rectas características de un plano son aquellas rectas del plano que son paralelas a los planos de proyección.
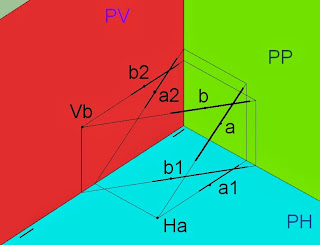
Por ejemplo, en el ejercicio siguiente, nos dan una recta frontal a y una recta horizontal b que como pertenecen a un mismo plano se cortan en un punto.
Para determinar el plano que pasa por ellas basta con prolongarlas hasta que corten a los planos de proyección, estos puntos serán las trazas de las rectas por donde pasan las trazas del plano.
En el caso particular de las rectas características del plano oblicuo, sólo necesitamos una traza de cada recta, ya que sabemos que la recta a es paralela a la traza vertical del plano, asimismo sabemos que la recta horizontal b es paralela a la traza horizontal del plano. Como tenemos las dos direcciones de las trazas, horizontal y vertical, sólo necesitamos las dos trazas de las rectas Ha y Vb para seguir esas dos direcciones y definir el plano. Sabemos además que el plano oblicuo corta a la línea de tierra en un punto, esto quiere decir que si por Ha hacemos la dirección b obtendremos un punto de intersección con la línea de tierra que uniremos con Vb, sin necesidad de conocer que por Vb pasada traza del plano paralela a la recta a y su proyección a2.
En el dibujo siguiente podemos ver la obtención de las trazas en el espacio: al prolongar la recta a corta al plano horizontal en Ha, esto que podemos ver en el espacio lo tenemos que dibujar en sistema diédrico en el alzado, y una vez que tenemos ese punto de intersección, que en el alzado es con la línea de tierra, bajamos una recta perpendicular a la línea de tierra hasta que corte a a1, obteniendo Ha. Por este punto pasa la traza del plano y es paralela a la proyección horizontal b1 de la recta b.
De igual forma prolongamos la recta b hasta que corta al plano vertical en un punto Vb, en el sistema diédrico tendremos que prolongar la proyección de esta recta hasta que corte a la línea de tierra en un punto por el que haremos una vertical que define en su intersección con b2 la traza vertical Vb del plano. Por Vb pasa la otra traza del plano que es paralela a la recta a y a su proyección a2.
A continuación observamos el ejercicio resuelto en el sistema diédrico: tenemos las dos rectas a b definidas por sus proyecciones y por su punto de intersección I determinado por sus proyecciones I1, I2, como ambas proyecciones están alineadas en una vertical quiere decir que ambas rectas se cortan y por tanto por ellas pasa un plano.
Prolongamos a2 hasta que corta a la línea de tierra en un punto T por el que bajamos una vertical que intercepta a a1 en Ha, ésta es la traza de la recta por la que pasa la traza del plano hg paralela a b1.
De igual forma prolongamos b1 hasta que corta a la línea de tierra en un punto P por el que levantamos una vertical que intercepta a la prolongación de b2 en el punto Vb, ésta es la traza vertical de la recta por la que pasa el plano y cuya traza es paralela a a2.
De esta forma hemos obtenido las dos trazas del plano que se cortan necesariamente en un punto de la línea de tierra ya que el plano corta a la línea de tierra en un punto y pertenece a la intersección de los dos planos de proyección, de ello se sigue que pertenece también a las trazas del plano.
Plano tangente a esfera en un punto
Para calcular un plano tangente a una esfera e incidente en un punto A, debemos saber que el plano es perpendicular a la recta que pasa por ese punto y por el centro de la esfera.
Por tanto por el punto A1 en planta pasamos una línea perpendicular h a OA Hasta que corta a la línea de tierra, por este punto de intersección levantamos una vertical hasta que corte a una horizontal que pasa por A2. En este punto de intersección de la vertical discontinua y h2 hacemos la traza del plano que sabemos que es perpendicular a A2-O2. Donde esta traza azul vertical del plano corta a la línea de tierra, hacemos otra línea perpendicular a A1-O1, esta línea es la traza horizontal del plano.
Plano tangente a un cono en un punto
Para hacer un plano tangente a un cono que pase un punto A del mismo, hacemos la generatriz g que pasa por ese punto y por el vértice V hasta que corte en la planta a la base de la figura.
Esta generatriz es la recta de máxima pendiente del plano que ya podemos construir, sabiendo que su traza Horizontal es perpendicular A la proyección en planta de la recta y que la traza vertical pasa por la intersección de esta traza horizontal con la línea de tierra y por la traza vertical de la recta.
 Para dibujar un cono apoyado en un plano de canto o proyectante vertical, dibujamos la dimensión de su diámetro sobre la traza vertical. A partir del centro de la base hacemos una perpendicular y tomamos su medida real correspondiente a la altura. Este vértice ya lo podemos proyectar en la planta y el perfil.
Para dibujar un cono apoyado en un plano de canto o proyectante vertical, dibujamos la dimensión de su diámetro sobre la traza vertical. A partir del centro de la base hacemos una perpendicular y tomamos su medida real correspondiente a la altura. Este vértice ya lo podemos proyectar en la planta y el perfil.Pirámide apoyada en plano oblicuo
 Para dibujar una pirámide apoyada en un plano Oblicuo, dibujamos su base abatida de color azul en el plano abatido, a continuación subimos las rectas de este cuadrado obteniendo la proyección en planta y alzado del mismo sobre el plano. En la intersección de las diagonales tenemos la base del segmento vertical ortogonal al plano, por lo que sus proyecciones son perpendiculares a las trazas del plano. Mediante un giro podemos observar la dimensión real de la altura, en el momento en el que la recta girada aparece paralela al plano vertical.
Para dibujar una pirámide apoyada en un plano Oblicuo, dibujamos su base abatida de color azul en el plano abatido, a continuación subimos las rectas de este cuadrado obteniendo la proyección en planta y alzado del mismo sobre el plano. En la intersección de las diagonales tenemos la base del segmento vertical ortogonal al plano, por lo que sus proyecciones son perpendiculares a las trazas del plano. Mediante un giro podemos observar la dimensión real de la altura, en el momento en el que la recta girada aparece paralela al plano vertical.
Dibujar un triángulo sobre un plano paralelo a la línea de tierra
 Dibujamos el plano paralelo a la línea de tierra y lo abatimos, dibujando su figura triangular en la parte superior. Al proyectar los vértices del triángulo sobre la línea vertical - intersección de los planos verticales de proyección- y hacer un giro de los mismos hasta que coinciden sobre la traza de perfil, obtenemos ya el perfil del triángulo cuyos puntos proyectamos mediante horizontales hasta obtener en la intersección con las verticales que pasan por cada uno de los puntos del triángulo la figura en alzado. El mismo procedimiento podemos seguir para obtener la figura en planta, por ejemplo proyectando los puntos del perfil sobre la línea de tierra y trasladando esas distancias mediante giros hasta obtener su vista en planta.
Dibujamos el plano paralelo a la línea de tierra y lo abatimos, dibujando su figura triangular en la parte superior. Al proyectar los vértices del triángulo sobre la línea vertical - intersección de los planos verticales de proyección- y hacer un giro de los mismos hasta que coinciden sobre la traza de perfil, obtenemos ya el perfil del triángulo cuyos puntos proyectamos mediante horizontales hasta obtener en la intersección con las verticales que pasan por cada uno de los puntos del triángulo la figura en alzado. El mismo procedimiento podemos seguir para obtener la figura en planta, por ejemplo proyectando los puntos del perfil sobre la línea de tierra y trasladando esas distancias mediante giros hasta obtener su vista en planta.Incidencia de dodecaedro e icosaedro en una misma proyección
http://el-numero-de-oro.blogspot.com/
Esfera circunscrita en tetraedro:
Vamos a obtener una esfera circunscrita a un tetraedro que puede ser irregular. Tal y como vemos en la figura de la derecha el tetraedro en color negro, trazamos dos circunferencias verdes que pasen por dos triángulos de la figura y esas dos circunferencias pertenecerán a la esfera que pasa por los vértices del tetraedro. Por tanto, una vez que tenemos las dos circunferencias trazaremos por sus centros perpendiculares que se cortarán en un punto, que será el centro de la esfera y su radio vendrá comprendido desde ese punto hasta cualquier vértice del tetraedro, ya que los cuatro van a pasar por la esfera.
Una vez que tenemos claro como se realiza en el espacio, pasamos al lado izquierdo al sistema diédrico, tenemos las dos proyecciones del tetraedro, abatimos la cara verde del tetraedro y obtenemos la cara violeta, pasamos la circunferencia por los tres puntos del triángulo y obtenemos en la intersección de dos cuerdas el centro P de ese triángulo que desabatimos y proyectamos sobre el alzado, trazando en ese punto la perpendicular "a" (en verde) por P'.
Hacemos lo mismo con la circunferencia de la planta que pasa por los tres vértices que se apoyan en el plano horizontal y tenemos la recta vertical b, que corta a la anterior (a) en el centro O de la esfera; por último tomamos como radio OS de la circunferencia meridiana del alzado, éste vendrá dado por la proyección vertical del punto S -obtenido al trazar una horizontal por b en la planta en el corte con la circunferencia azul- y el centro O.
Una vez que la tenemos en el alzado la proyectaremos también a la planta para tener las dos vistas de la esfera circunscrita al tetraedro irregular.
Esfera inscrita en tetraedro:
Tenemos un tetraedro en color azul en sistema diédrico a la izquierda, se trata de inscribir una esfera azul en su interior de manera que sea tangente a las cuatro caras.
En el alzado tenemos la línea de máxima pendiente P2 de la cara a la izquierda y lo que hacemos es la bisectriz b a esa línea y a la línea de tierra. En la intersección con un segmento e de una altura cualquiera, obtenemos un punto que proyectamos mediante una línea vertical h sobre la planta obteniendo entonces el primer lado de un triángulo negro que podemos observar en planta, triángulo que tiene los 3 lados paralelos al triángulo azul de la base del tetraedro.
Hacemos lo mismo con las otras dos proyecciones de las otras caras, mediante cambios de plano, de manera que la línea de tierra para el caso izquierdo es de color naranja y para el caso derecho de color verde.
En el caso izquierdo en naranja volvemos a hacer la bisectriz de la línea de máxima pendiente p1 con la línea de tierra naranja, obteniendo la línea roja que con la intersección con una línea paralela a la línea de tierra naranja y de igual altura que e -caso anterior- nos genera un punto por el que trazamos una paralela g al lado del triángulo azul NÑ de esta manera obtenemos otro lado del triángulo negro, el lado RS.
Por último a la derecha hacemos la nueva proyección en el nuevo cambio de plano de línea de tierra verde; la línea de máxima pendiente de la cara MÑO que es la línea p3 y hacemos la bisectriz de la línea de tierra verde y de esta línea de máxima pendiente p3 obteniendo la línea C que cortada por una paralela f a la misma altura que en los otros dos casos, obtenemos un punto de intersección desde el que trazamos una perpendicular i a la línea de tierra verde, de manera que obtenemos el lado del triángulo J. Una vez que ya tenemos este triángulo negro que es una sección horizontal de los tres planos bisectores de las caras laterales del triedro y su base, unimos 2 de sus vértices RS con los vértices respectivos del triángulo NÑ de la base del tetraedro, de manera que la intersección de estas líneas nos genera el punto central de la esfera O. Lo subimos mediante una vertical hasta que corte en el alzado a la prolongación de la línea b,. de esta manera obtenemos el centro O2 de la esfera y cuyo radio es O2-Y, ya que la esfera se apoya en la base de la figura por lo que será tangente a las cuatro caras del tetraedro regular, incluida la base.




















No hay comentarios:
Publicar un comentario